Explore

The FUNdamental Theorem of Algebra Solutions

• The Fundamental Theorem of Algebra states: Every polynomial equation with    complex    coefficients and    positive    degree n has    exactly n    complex roots.
• Which means:
  • $\underline{\mathbf{ }\mathbf{ }\mathbf{ }\mathit{n}\mathbf{\ge }\mathbf{1}\mathbf{ }\mathbf{ }\mathbf{ }}$, and there are exactly n complex roots (including multiplicities).
  • If $\underline{\mathbf{ }\mathbf{ }\mathbf{ }\mathit{a}\mathbf{+}\mathit{b}\mathit{i}\mathbf{ }\mathbf{ }\mathbf{ }}$ is a root, then $\underline{\mathbf{ }\mathbf{ }\mathbf{ }\mathit{a}\mathbf{–}\mathit{b}\mathit{i}\mathbf{ }\mathbf{ }\mathbf{ }}$ must also be a root, when a and b are real numbers and $b\ne 0$.
    • In other words, complex roots occur in    conjugate pairs   .
• The FTA tells you the    total number of roots   .  
  • Polynomials can have real and non-real, complex roots, but the roots must have a    combined total equal to   the $n^{\mathrm{th}}$ degree of the polynomial.
  • You must continue to solve until you find    all n roots   , remembering to include multiplicities.
• Solving for roots with the FTA allows you to determine:
  • All    n roots   .
  • If a root is    real   and will intersect the x-axis.
  • If a root is    non-real, complex   , and will not intersect the x-axis.

Note

We are only graphing or sketching intercepts on the real coordinate plane.

$f\left(x\right)=A{x}^5+B{x}^4+C{x}^3+D{x}^2+Ex+F$

Degree	Real	Non-Real, Complex	Sketch (with multiplicities of 1)
5	5	0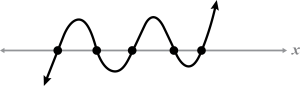
	4	1	not possible
	3	2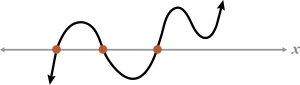
	2	3	not possible
	1	4
	0	5	not possible

$g\left(x\right)=A{x}^4+B{x}^3+C{x}^2+Dx+E$

Degree	Real	Non-Real, Complex	Sketch (with multiplicities of 1)
4	4	0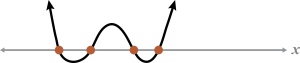
	3	1	not possible
	2	2
	1	3	not possible
	0	4	not possible

Example 1

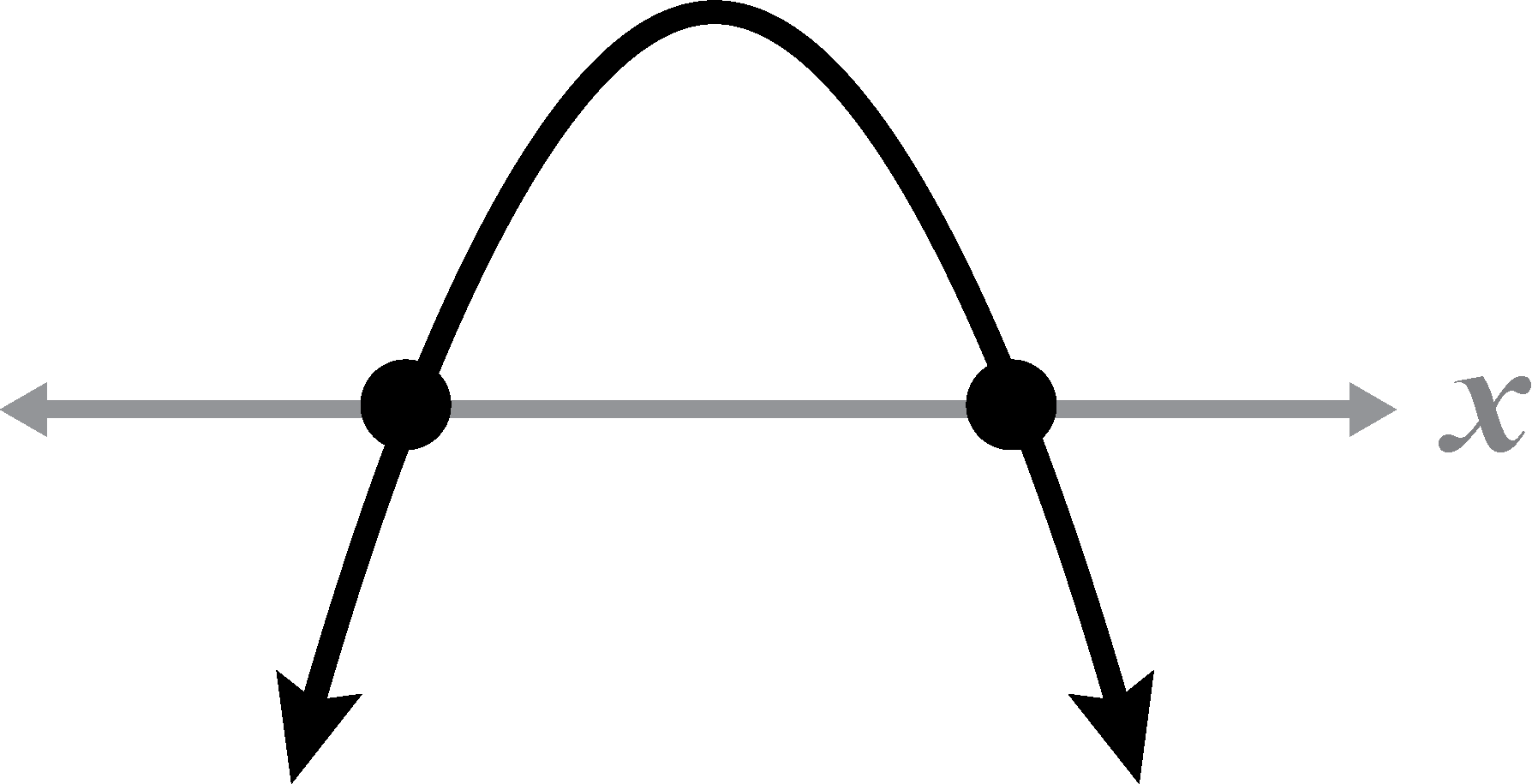
Given the sketch of a 2nd degree polynomial, determine if a is greater than or less than zero, and if the roots are real or non-real, complex.

Example 2

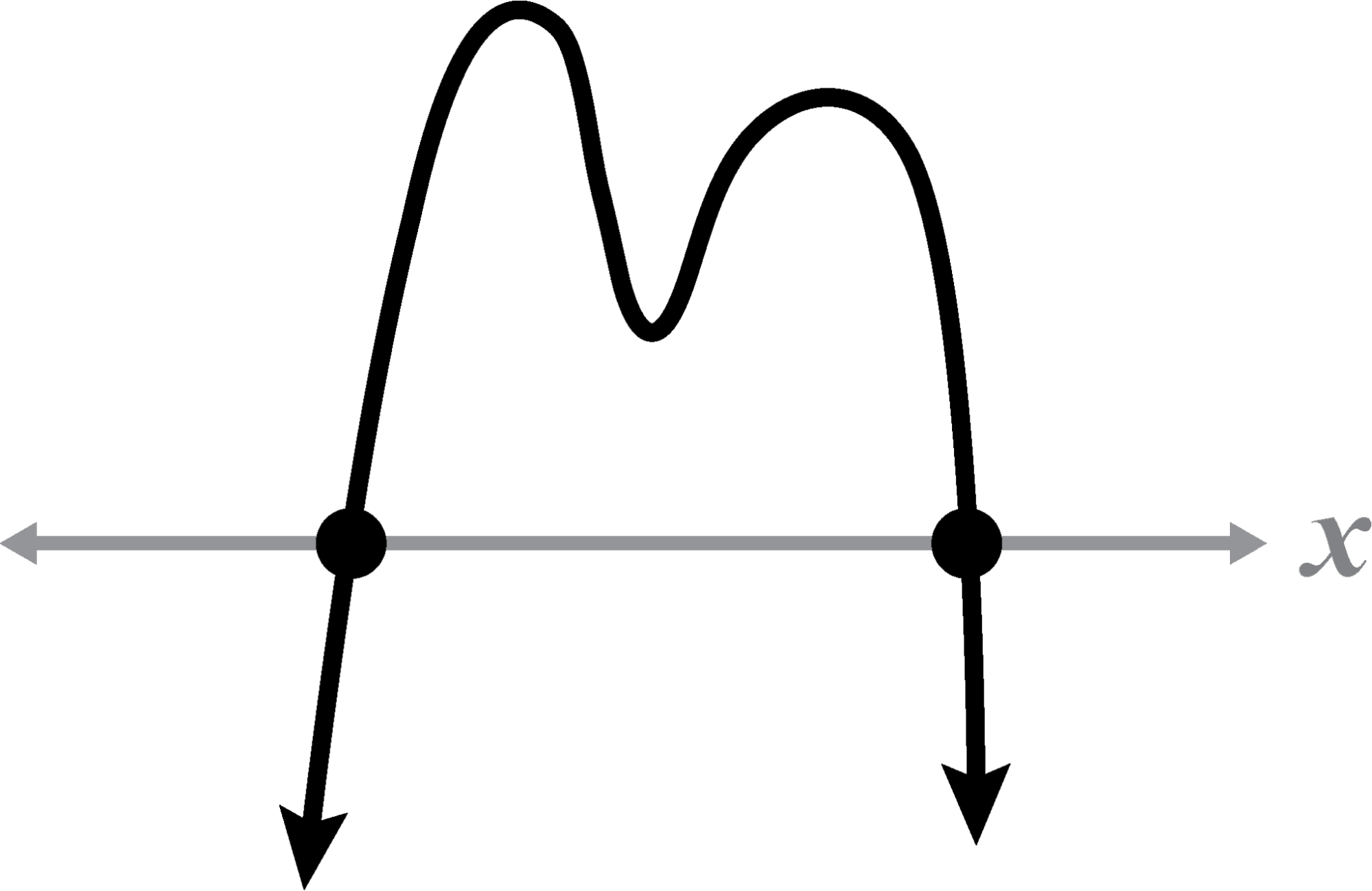
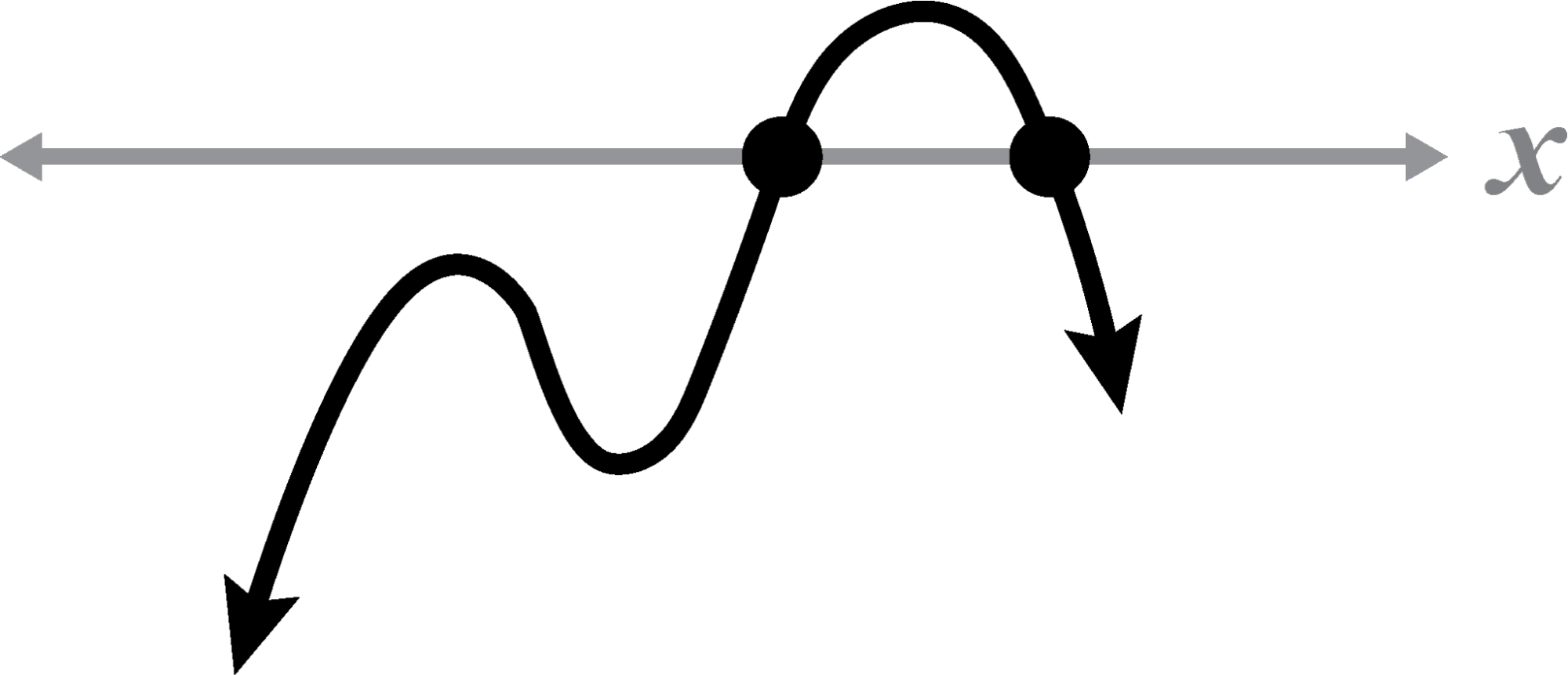
Given a 4th degree polynomial $(\mathit{n}=4)$ where $\mathit{a}\mathbf{<}\mathbf{0}$, identify the sketch(es) with 2 real roots with multiplicities of 1. If a sketch does not meet these criteria, explain why.

Note

If the degree is 4 and there are only 2 real roots, then there are two (a conjugate pair) of non-real, complex roots.

 

Use a table if necessary to organize possible combinations of real and non-real, complex numbers.