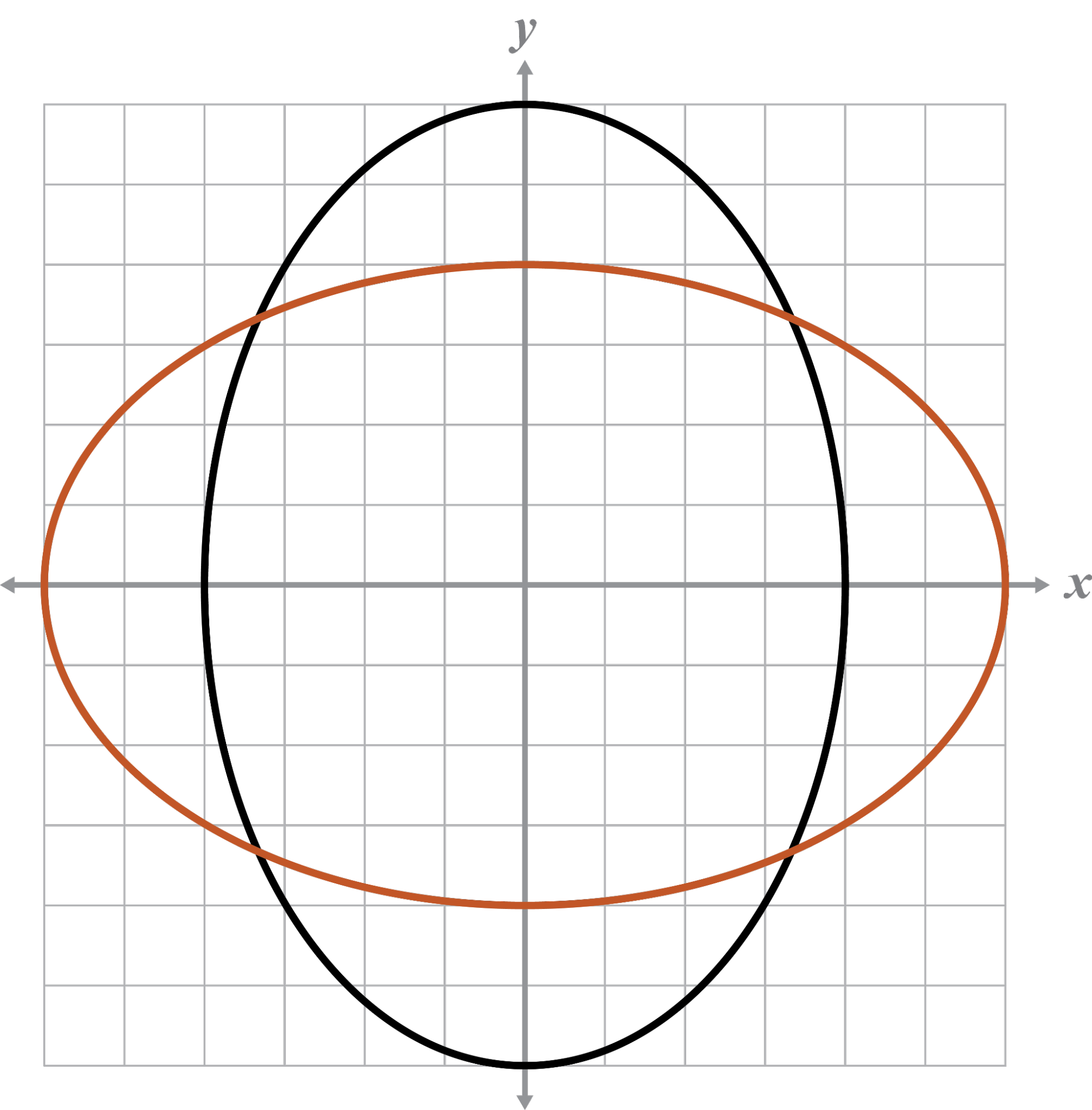
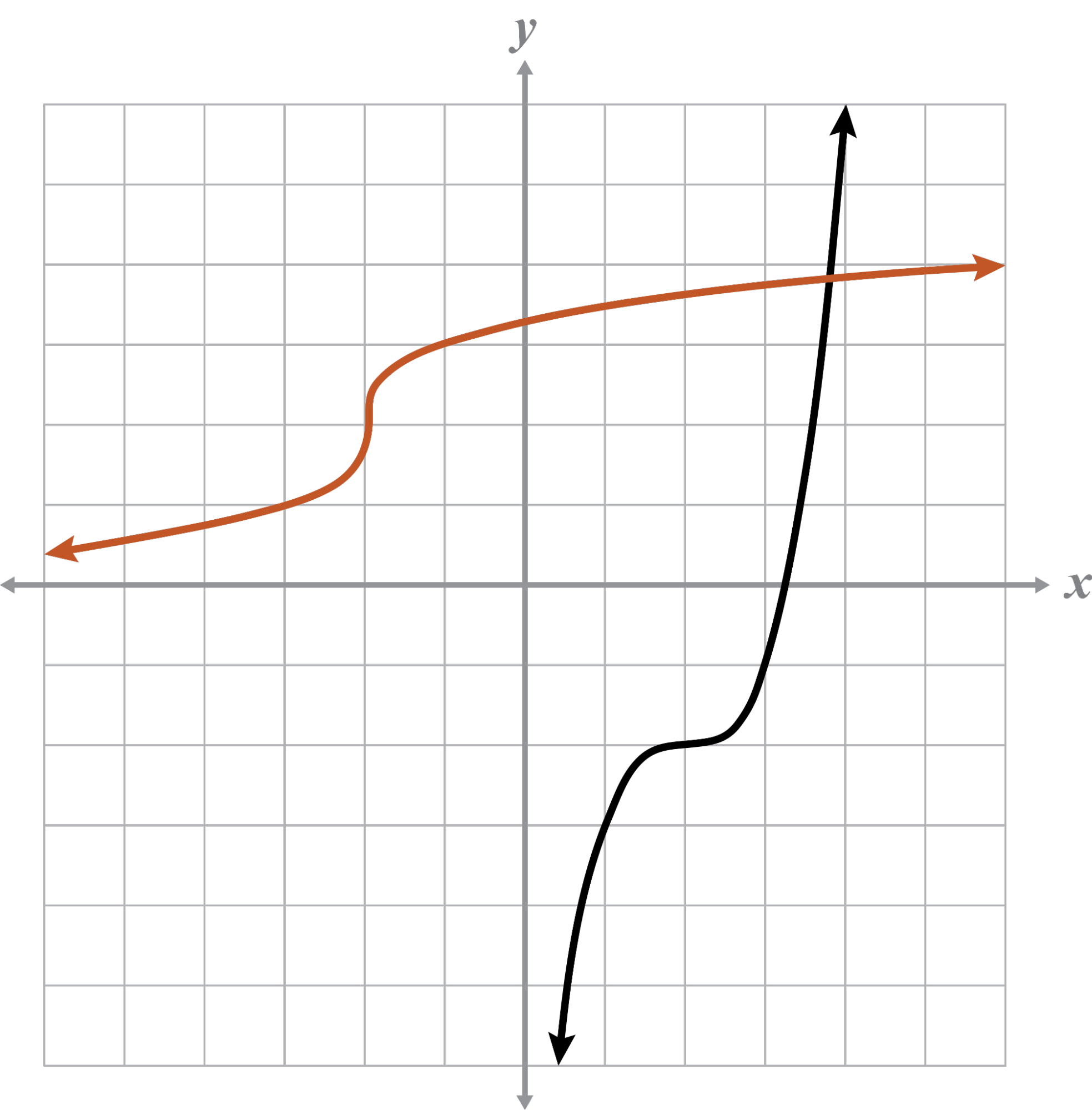
Practice 2 Solutions

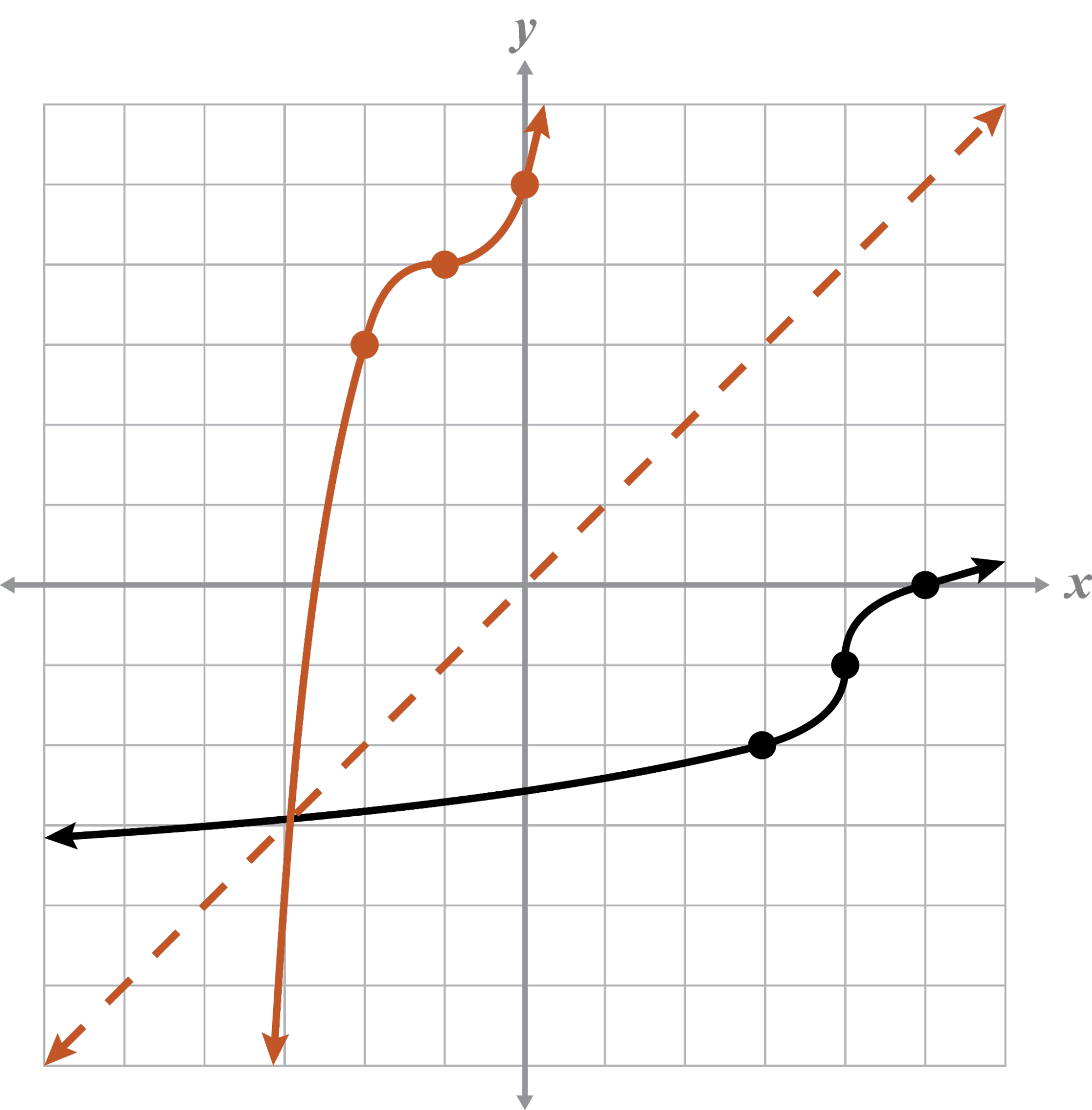
Graph the inverse on the coordinate plane.

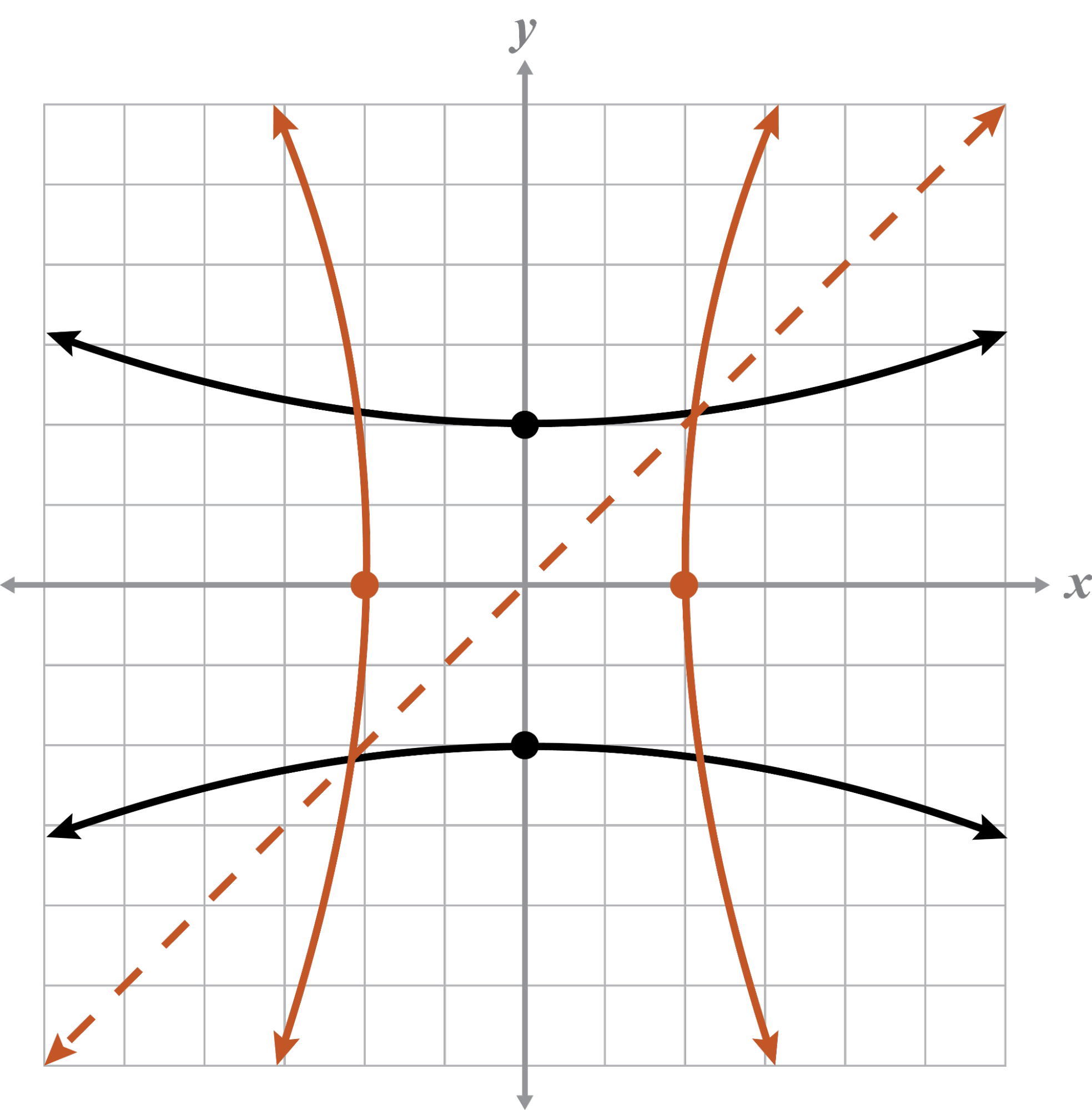
Graph the inverse on the coordinate plane. Explain whether or not the graph and its inverse represent functions.

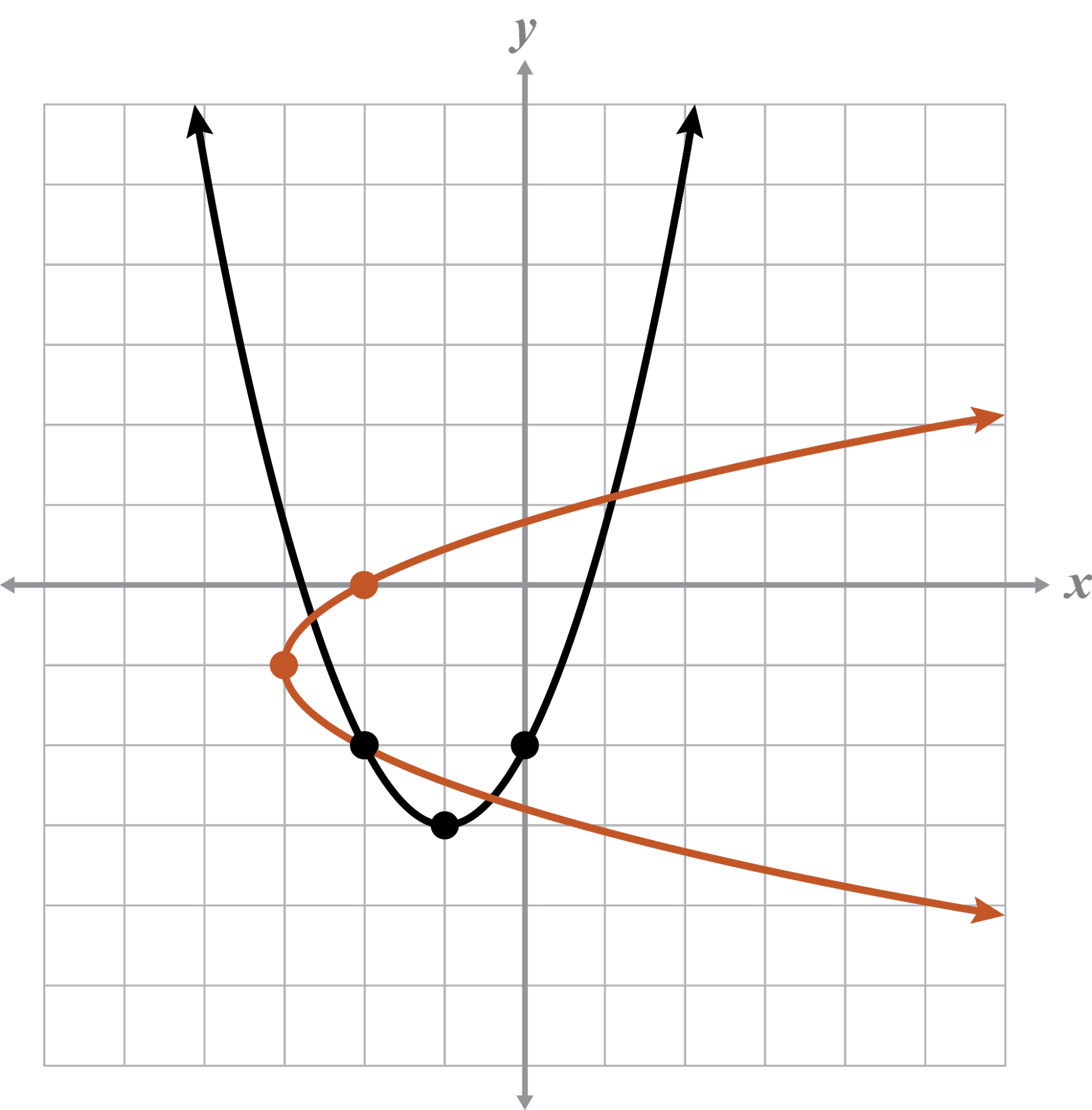
The given graph is a function because it passes the VLT.
The inverse of the graph is not a function because it fails the VLT.

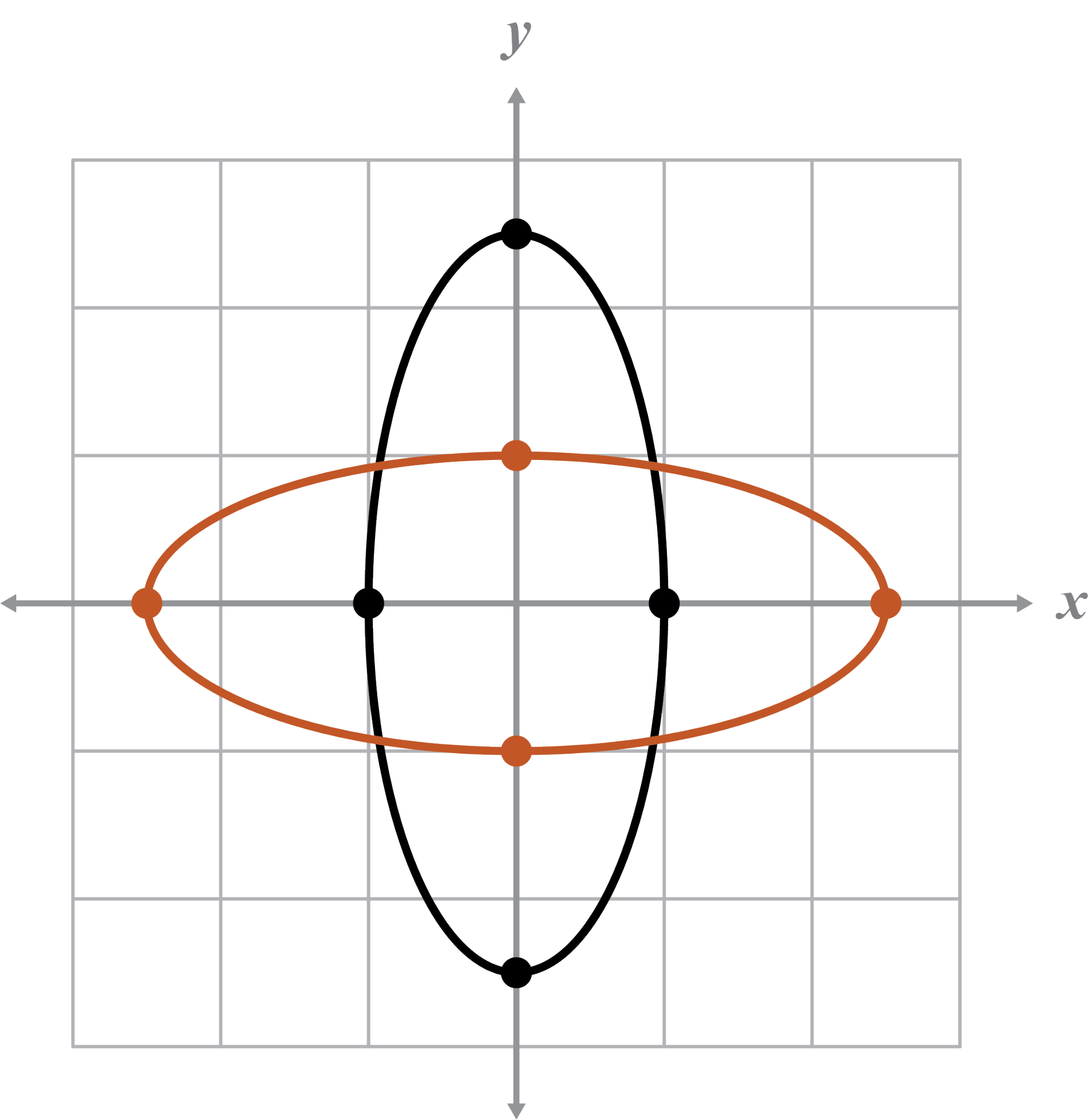
The given graph and the inverse are not functions because they do not pass the VLT.

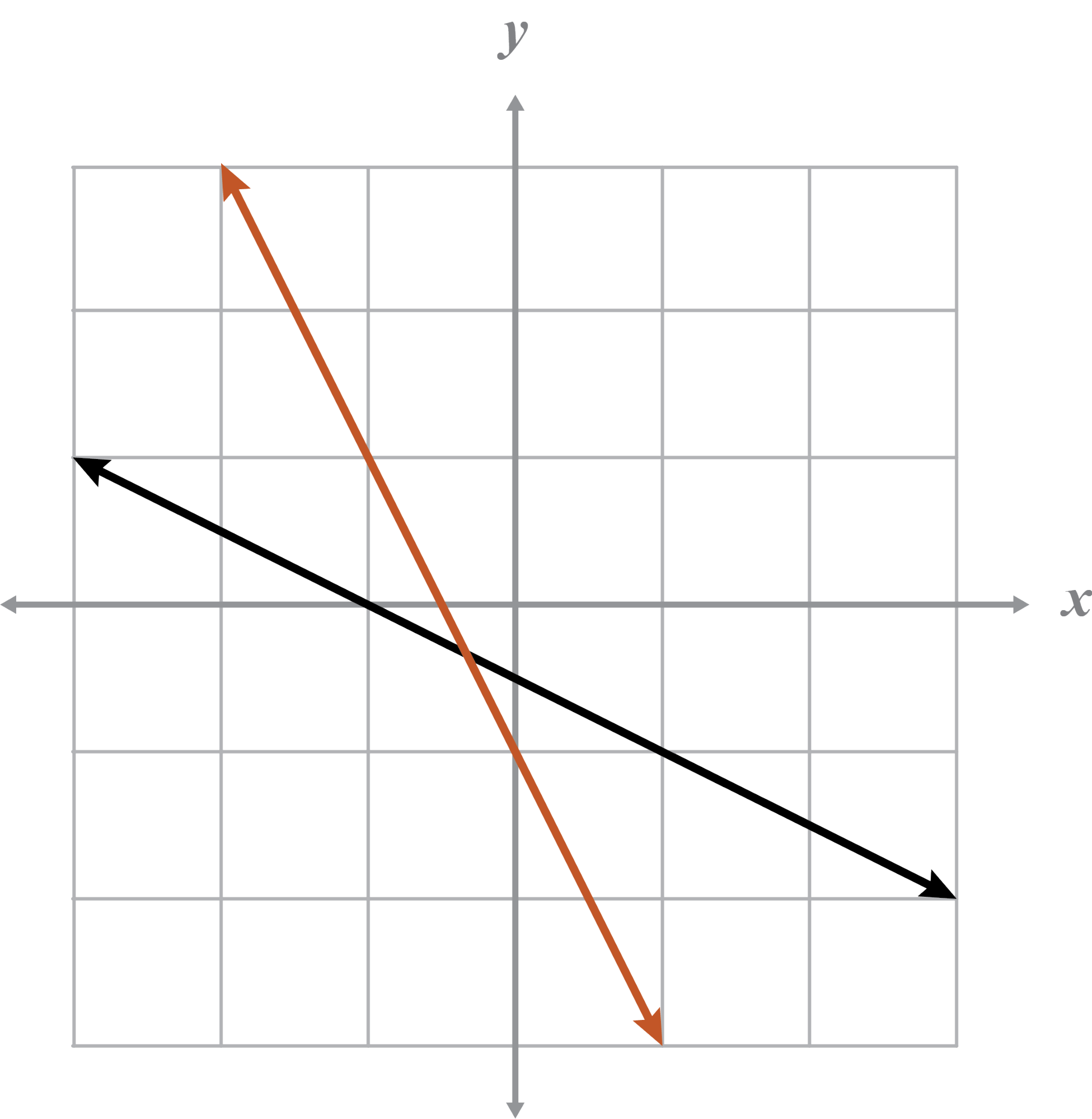
The given graph and the inverse are functions because they pass the VLT.

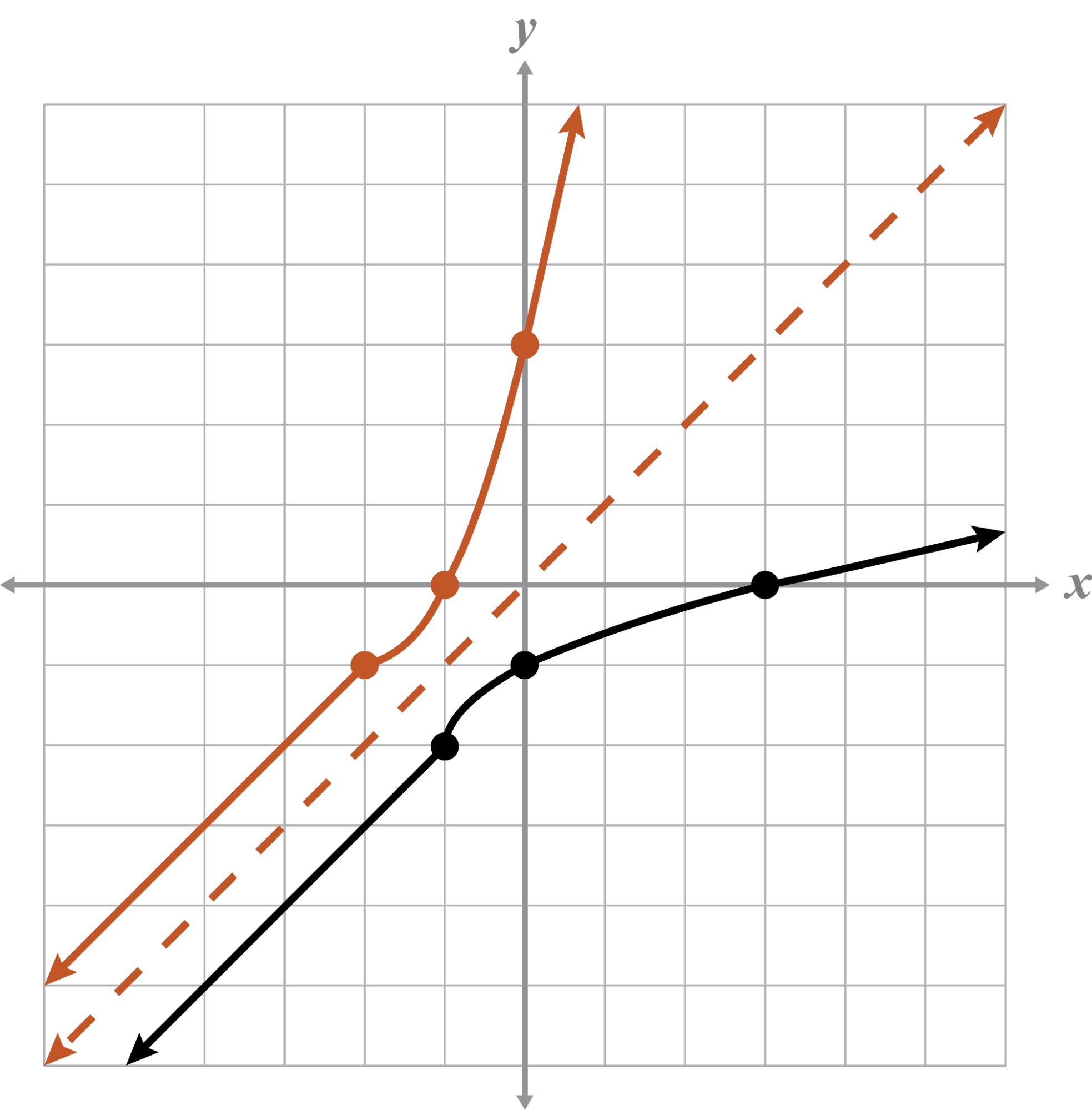
Find the inverse of the function algebraically. Then graph the function and its inverse on the coordinate plane. Explain whether or not the graph and its inverse represent functions.

$h (x) = \sqrt[3]{x - 2} + 1$

  $\begin{array}{rcl} x & = & \sqrt[3]{y - 2} + 1 \\ x - 1 & = & \sqrt[3]{y - 2} \\ {(x - 1)}^{3} & = & y - 2 \\ y & = & {(x - 3)}^{3} + 2 \end{array}$

$\begin{array}{rcl} h^{- 1} (x) & = & {(x - 1)}^{3} + 2 \end{array}$  

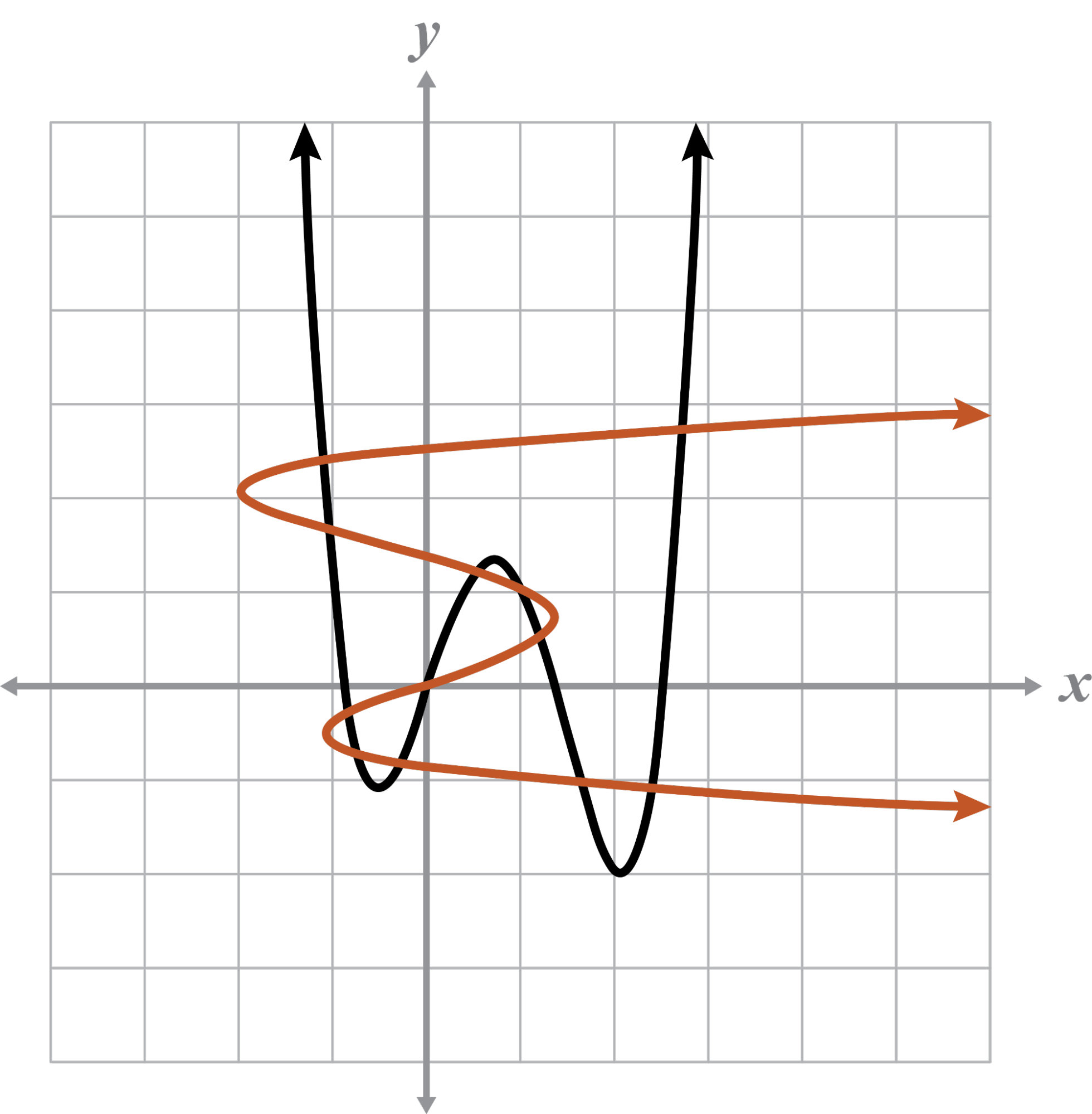
The given graph and the inverse are functions because they pass the VLT.

$g (x) = 2 \sqrt{x - 2} + 1 for \{x | x \geq 2\}$

  $\begin{array}{rcl} x & = & 2 \sqrt{y - 2} + 1 \\ x - 1 & = & 2 \sqrt{y - 2} \\ \frac{x - 1}{2} & = & \sqrt{y - 2} \\ \frac{1}{4} {(x - 1)}^{2} & = & y \end{array}$  

$\begin{array}{rcl} g^{- 1} (x) & = & \frac{1}{2} {(x - 1)}^{2} \{x | x \geq 1\} \end{array}$  
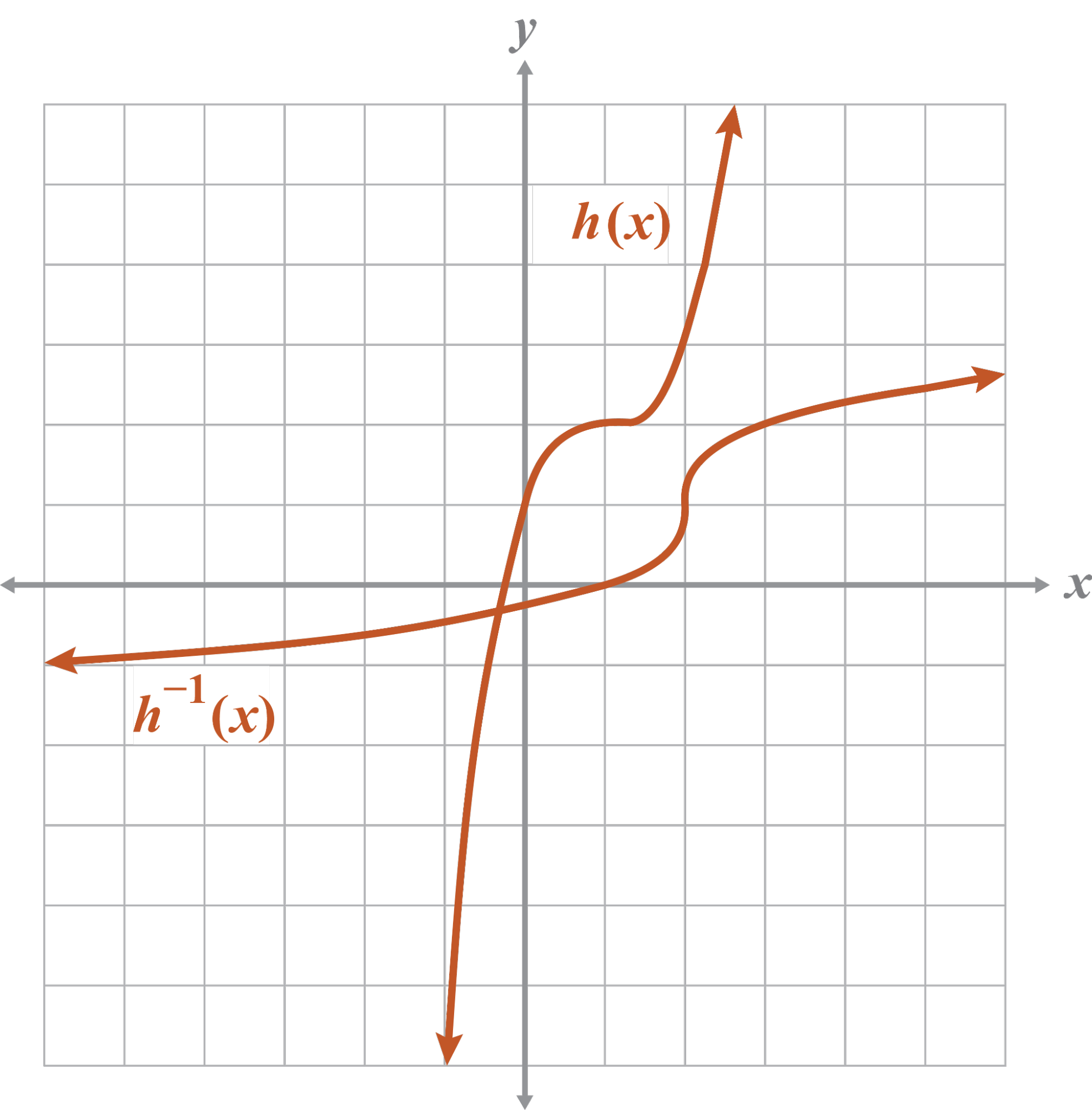
The given graph and the inverse are functions because they pass the VLT.

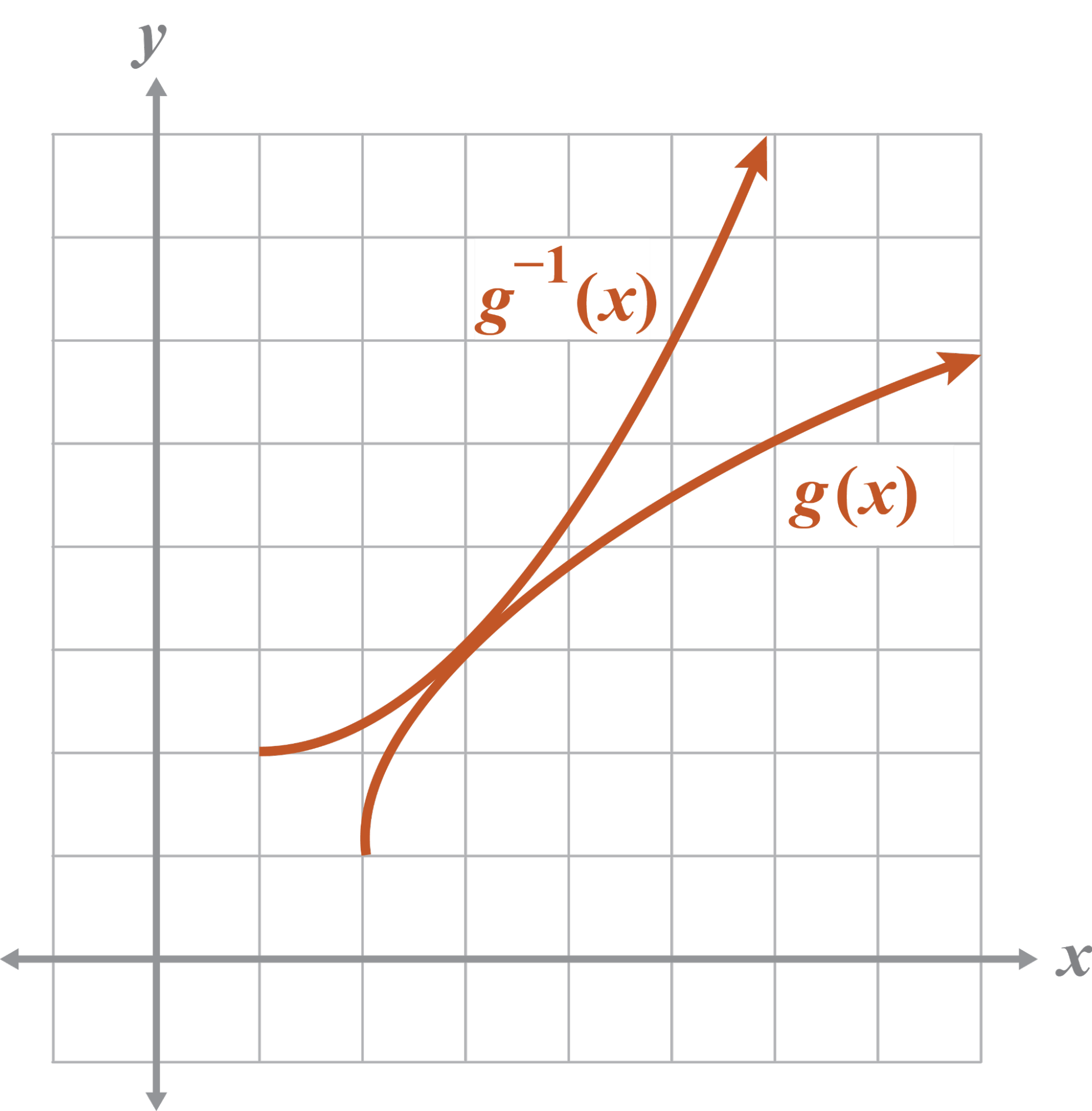
Note

Since g(x) is a square root function and has a domain restriction, $g^{- 1} (x)$ will also have a domain restriction. The domain of $g^{- 1} (x)$ is the range of g(x).

$f (x) = - x^{2} - 1$
  $\begin{array}{rcl} x & = & - y^{2} - 1 \\ x + 1 & = & - y^{2} \\ - (x + 1) & = & y^{2} \\ - x - 1 & = & y^{2} \\ \pm \sqrt{- x - 1} & = & y \end{array}$  

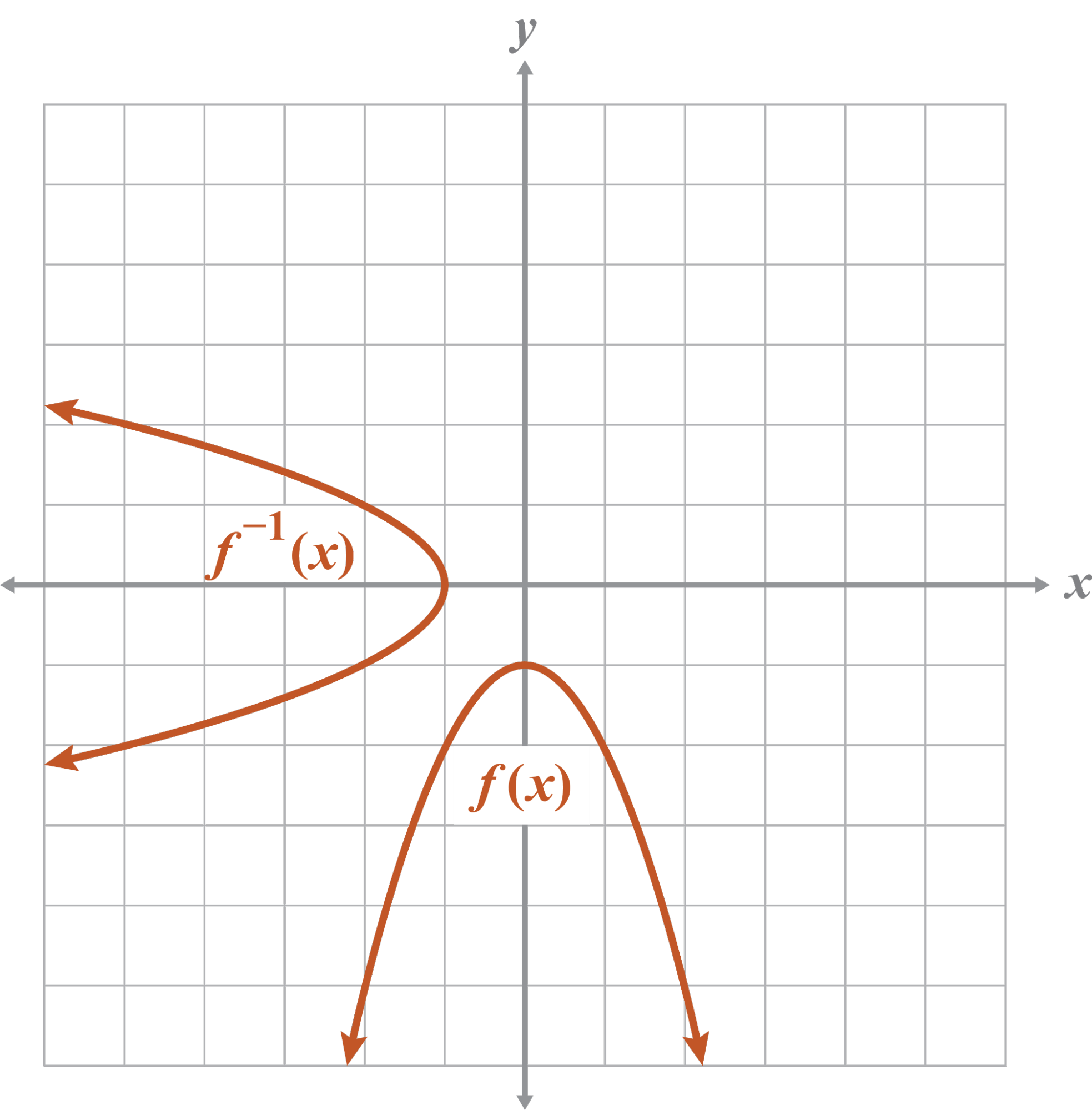
The given equation is a function, but the inverse is not a function because it does not pass the VLT.

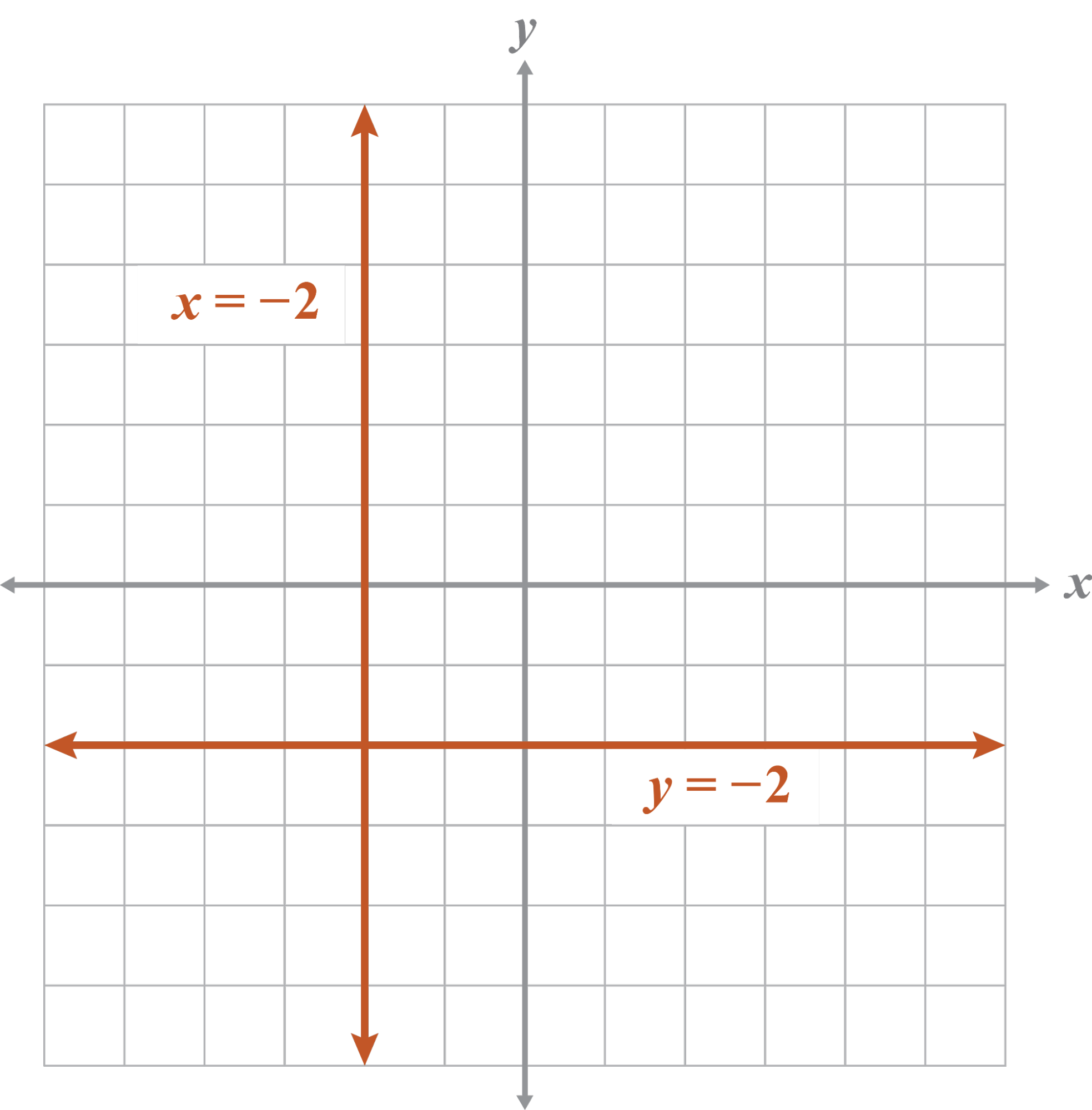
x = –2 
y = –2 
The given equation is not a function because it does not pass the VLT. The inverse is a function.

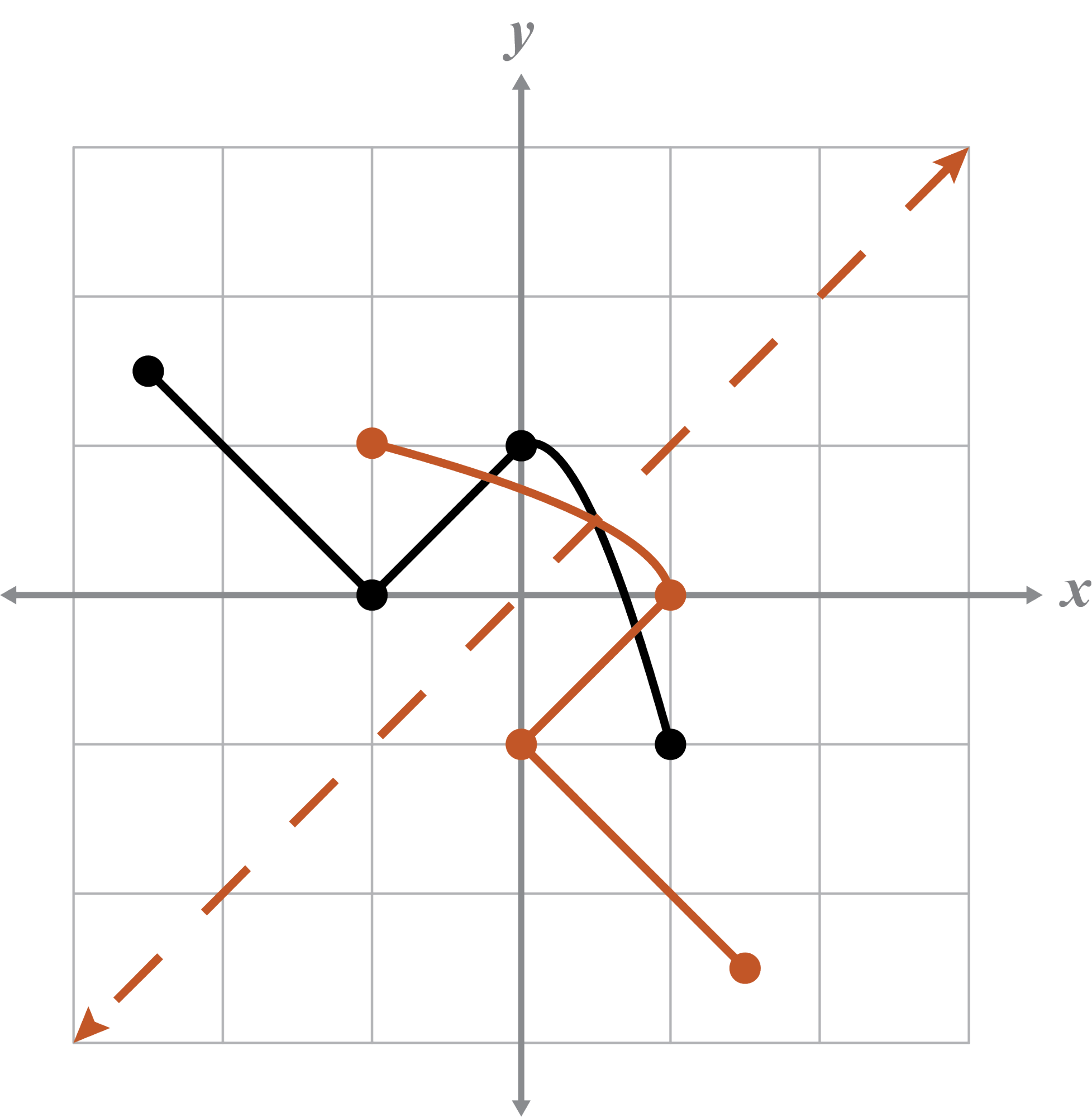
For the given graph: 

- Name the domain and range for the graph and its inverse.
- Explain whether or not the graph represents a function. 
- If the graph is a function, determine if it is one-to-one. 
- If the graph is a function, determine if the inverse is also a function.

Given 
Domain: $\{\begin{array}{rcl} x | x & \in & R \end{array}\}$  
Range: $\{\begin{array}{rcl} y | y & \geq & - 2 \end{array}\}$  

Inverse 
Domain: $\{\begin{array}{rcl} x | x & \geq & - 2 \end{array}\}$  
Range: $\{\begin{array}{rcl} y | y & \in & R \end{array}\}$  

f(x) is a function, but is not one-to-one because it fails the HTL. The inverse is not a function because the inverse fails the VLT.

Given 
Domain: $\{\begin{array}{rcl} x | - 4 & \leq & x \leq 4 \end{array}\}$  
Range: $\{\begin{array}{rcl} y | - 6 & \leq & y \leq 6 \end{array}\}$  

Inverse 
Domain: $\{\begin{array}{rcl} x | - 6 & \leq & x \leq 6 \end{array}\}$  
Range: $\{\begin{array}{rcl} y | - 4 & \leq & y \leq 4 \end{array}\}$  

The graph is not a function because it fails the VLT. The inverse is not a function because the inverse fails the VLT.

Given 
Domain: $\{\begin{array}{rcl} x | x & = & 3 \end{array}\}$  
Range: $\{\begin{array}{rcl} y | y & \in & R \end{array}\}$  

Inverse 
Domain: $\{\begin{array}{rcl} x | x & \in & R \end{array}\}$  
Range: $\{\begin{array}{rcl} y | y & = & 3 \end{array}\}$  

The graph is not a function because it fails the VLT. The inverse is a function because the inverse passes the VLT.

Given 
Domain: $\{\begin{array}{rcl} x | x & \in & R \end{array}\}$  
Range: $\{\begin{array}{rcl} y | y & \in & R \end{array}\}$  

Inverse 
Domain: $\{\begin{array}{rcl} x | x & \in & R \end{array}\}$  
Range: $\{\begin{array}{rcl} y | y & \in & R \end{array}\}$  

f(x) is a function and is one-to-one because it passes the HLT. The inverse is a function because the inverse passes the VLT.