Explore
Transformations of Parent Functions Solutions
Note
Transformations of linear and quadratic functions are covered in Algebra 1. These transformations will be in the practice problems, but will not be in the examples. Transformations of reciprocal functions were covered in the previous unit.
Function Name
General Form of the Function
Linear
Note
This is point-slope form with added to the right side of the equation.
Absolute Value
Quadratic
Square root
For these functions, the ordered pair is used to determine the parts of the domain, range, and end behavior
Cubic
Cube root
Rational
Note
In addition to “across” and “over,” be aware that the word “about” is also commonly used to describe reflection.
Note
This lesson will only reflect the square root function over the y-axis.
Note
Remember to use your notes and Formula Sheet to remind yourself what the parent graphs look like on the coordinate plane.
See the More to Explore activity to learn about using technology to transform graphs.
Example 1
Name the type of function. Then write the equation and explain the given transformation.
Plan
Name the type of function
Mark key points on given graph
Sketch the parent graph
Identify a, h, k
Write the equation
Implement
Type of function: Absolute value,
Identify a, h, k:
Equation:
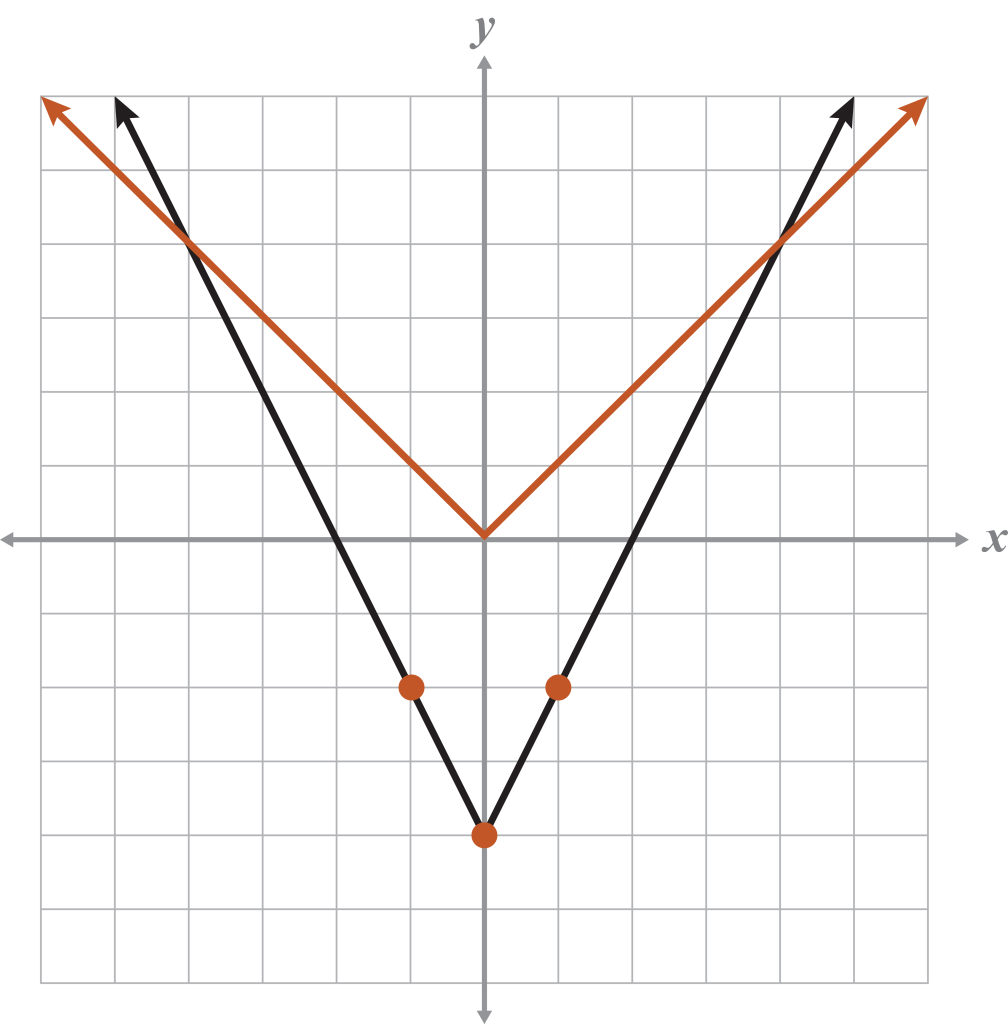
Explain
The graph stretches vertically by a factor of 2 and translates down 4 spaces as compared to the absolute value parent function. This occurs because , and
Note
Sketching the parent function is optional but provides a good frame of reference for transformations and determining the values of a, h, and k.
Example 2
Name the type of function. Then write the equation and explain the given transformation.
The cubic graph is a reflection with a horizontal translation left 2 spaces and a vertical translation up 1 space.
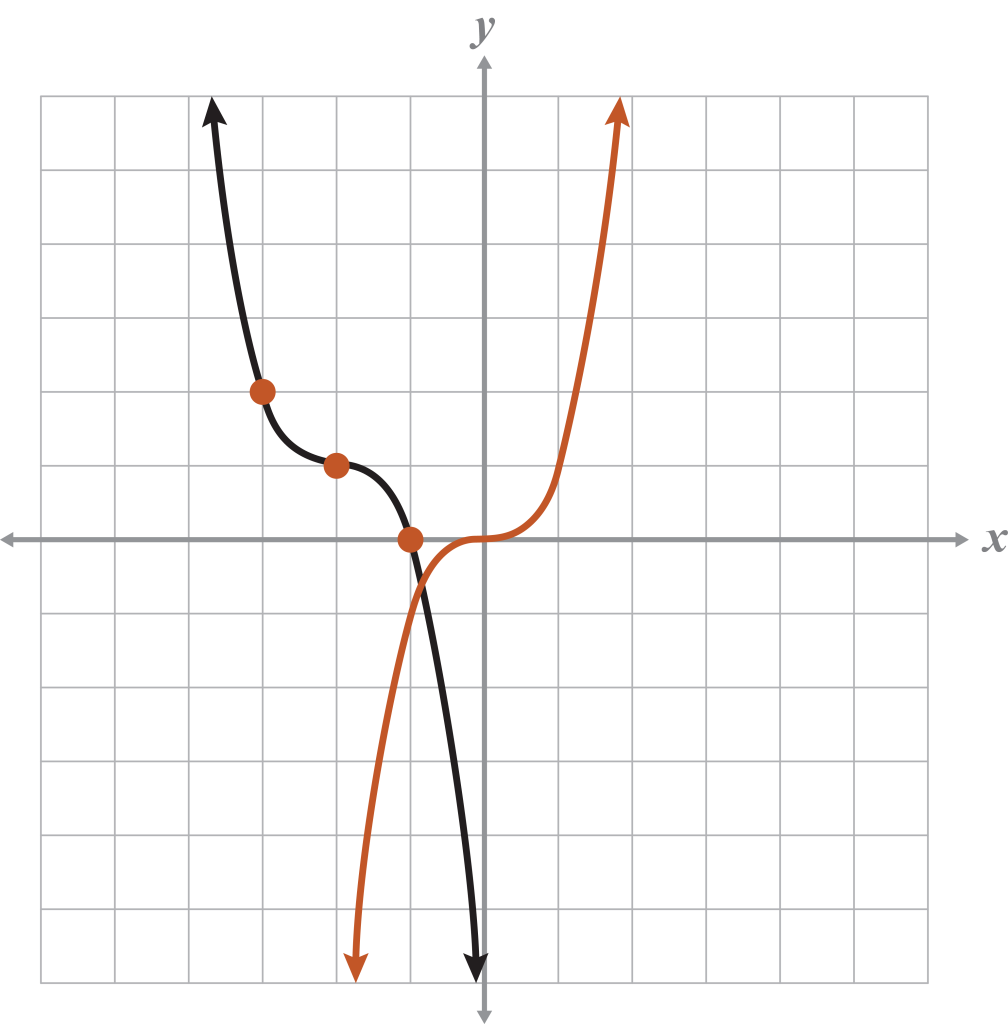
Note
Sketching the parent function is helpful because it is used to compare the transformed function to the parent graph. In this case, the end behavior changes for the y-values, which means that .
Example 3
Use the equation to name the type of function and describe the transformations occurring to the parent function.
: reflect over the y-axis
The square root function would reflect over the y-axis because .
The graph would be compressed vertically by a factor of because
The function would also shift right 12 units and shift up 7 units because
Note
If you are unsure of the direction for the horizontal translation, rewrite the radicand as You can also use technology to confirm the description based on the given equation.
