Explore

Solving Square Root Inequalities Solutions

Radical inequalities are solved using the same steps as radical equations.
Recall that when you multiply or divide by a negative number, the direction of the inequality symbol changes .
Because inequalities represent a set of values as the solution, it is important to check that all values are true for the radicand as well as the entire inequality.
Before solving square root inequalities, first check the radicand for principal root restrictions , because the principal root is a non-negative.
- Set each radicand to $\geq 0$ then solve.
Now, solve the given inequality .
- Compare the radicand inequalities to the solution to determine which combination of the results produces the most restrictive answer.
- Any result that is found outside of the most restricted combination is extraneous .
- If the solution is false for the restrictions of the principal root, there is no solution .

Note

Naming the restrictions for the radicand is also a step in graphing square roots and finding the domain, which will be covered later in this level.

Example 1

Solve. Graph the solution on a number line.

$2 + \sqrt{5 x + 10} < 7$

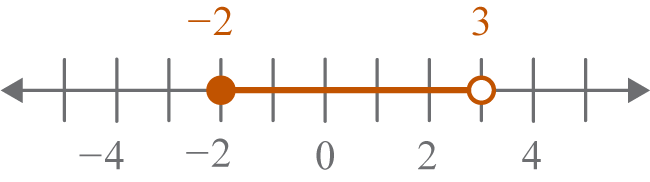
Implement

Restrictions

$\begin{array}{rcl} 5 x + 10 & \geq & 0 \\ 5 x & \geq & - 10 \\ x & \geq & - 2 \end{array}$

Solve

$\sqrt{5 x + 10} < 5 {(\sqrt{5 x + 10})}^{2} < {(5)}^{2}$

$\begin{array}{rcl} 5 x + 10 & < & 25 \\ 5 x & < & 15 \\ x & < & 3 \\ - 2 \leq x < 3 \end{array}$

Explain

All values must be greater than or equal to – 2 so that the principal root is true
Isolate the radical expression
Square both sides
Solve for x
Use the restriction on the radicand and the answer to the given problem to determine all solutions

Note

Use mental math to check values ≥ 2, between – 2 and 3, and < 3 to confirm answers.

Using a calculator to check can be helpful so that decimal values can be compared rather than fractions with uncommon denominators.

Example 2

Solve. Graph the solution on a number line.

$\sqrt{2 x - 2} \geq \sqrt{5 x}$

Implement

Restrictions

$\begin{array}{rcl} \begin{matrix} 2 x - 2 \geq 0 & 5 x \geq 0 \\ 2 x \geq 2 & x \geq 0 \\ x \geq 1 \end{matrix} \end{array}$

Explain

The restriction should be true for both radicand inequalities.

Solve

$\begin{array}{rcl} {(\sqrt{2 x - 2})}^{2} & \geq & {(\sqrt{5 x})}^{2} \\ 2 x - 2 & \geq & 5 x \\ - 2 & \geq & 3 x \\ x & \leq & - \frac{2}{3} \end{array}$

No solution

x cannot be greater than 1 and less than $- \frac{2}{3}$ at the same time.

Example 3

Solve. Graph the solution on a number line.

$8 + \sqrt{2 x - 5} \geq 3$

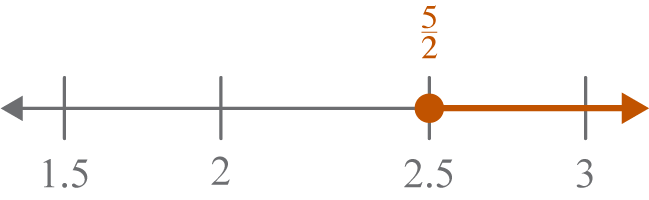
Restrictions

$\begin{array}{rcl} \begin{matrix} 2 x - 5 \geq 0 \\ 2 x \geq 5 \\ x \geq \frac{5}{2} \end{matrix} \end{array}$

What if the inequality was ≤ ?

$\sqrt{2 x - 5} \leq - 5 No solution$

Solve

$\sqrt{2 x - 5} \geq - 5$

The principal root will always be greater than a negative number.

Note

The restriction for the radicand is the solution.

Note

The principal square root is positive and a positive number cannot be less than or equal to a negative number.

Example 4

Solve. Graph the solution on a number line.

$\sqrt{x + 6} \geq 2 - \sqrt{x}$

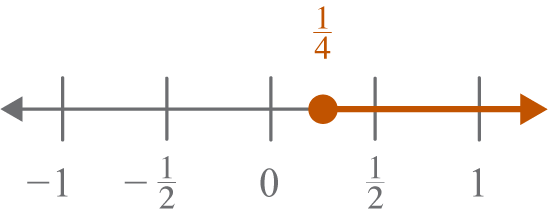
Restrictions
$\begin{matrix} x \geq - 6 & x \geq 0 \end{matrix}$

Check

$\begin{array}{rcl} \sqrt{6.25} & = & 2.5 \\ 2 - \sqrt{0.25} & = & 1.5 \\ 2.5 & > & 1.5 ✓ \end{array}$

Solve

$\begin{array}{rcl} {(\sqrt{x + 6})}^{2} & \geq & {(2 - \sqrt{x})}^{2} \\ x + 6 & \geq & (2 - \sqrt{x}) (2 - \sqrt{x}) \\ x + 6 & \geq & 4 - 4 \sqrt{x} + x \\ 2 & \geq & - 4 \sqrt{x} \\ - \frac{1}{2} & \leq & \sqrt{x} \\ {(- \frac{1}{2})}^{2} & \leq & {(\sqrt{x})}^{2} \\ x & \geq & \frac{1}{4} \end{array}$

Note

Use $x \geq \frac{1}{4}$ because this produces the most restrictive answer.