Practice 2 Solutions

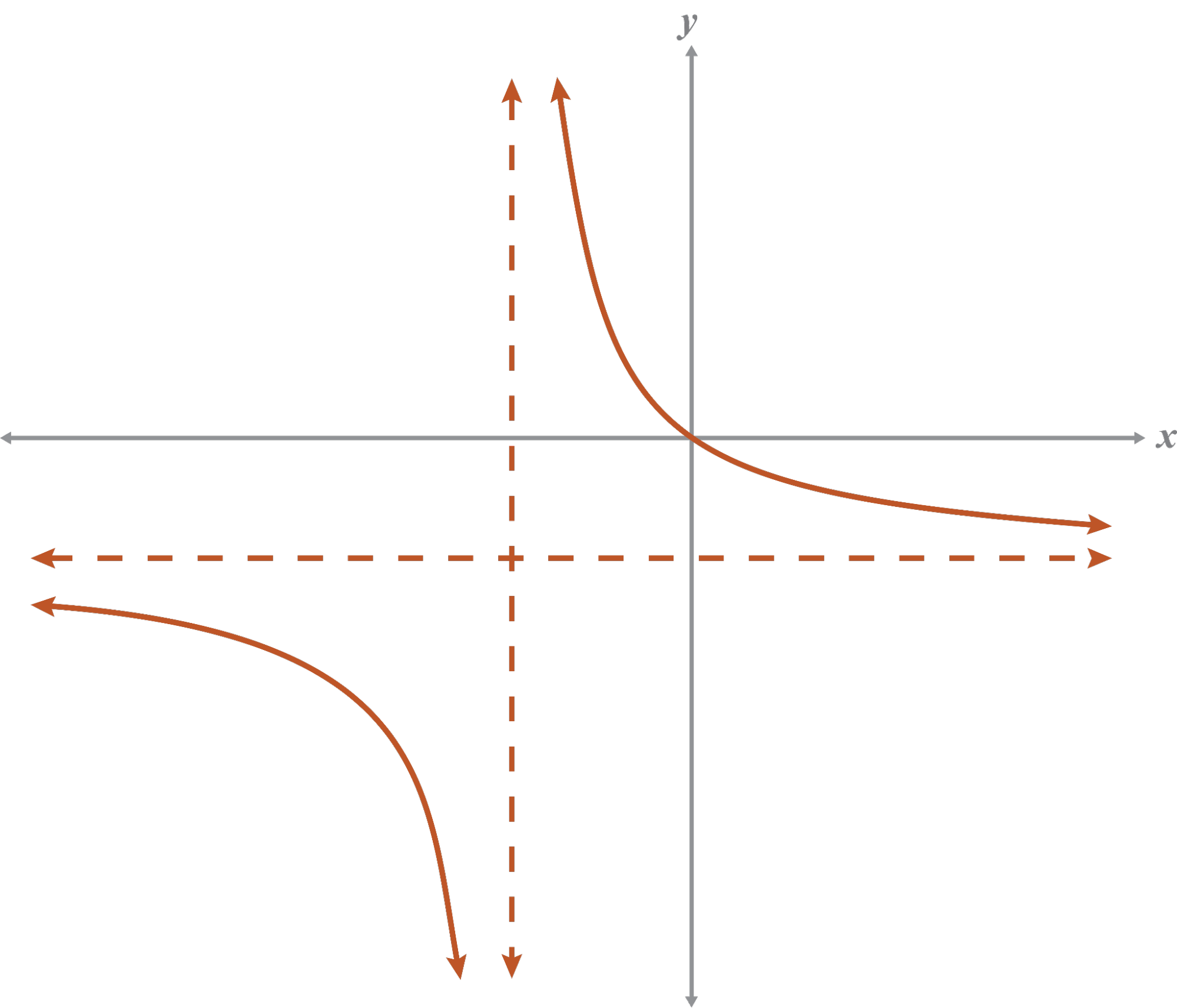
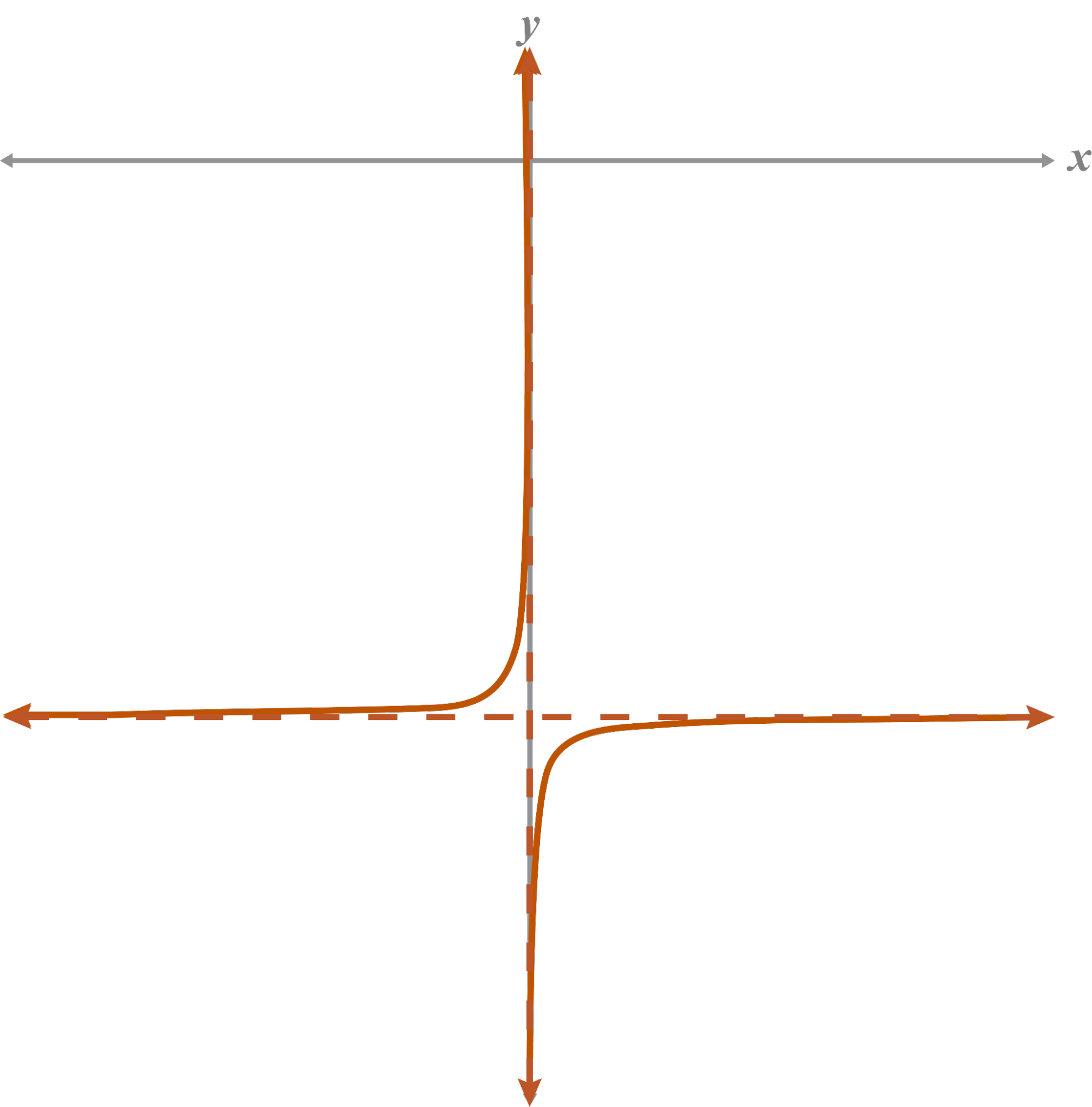
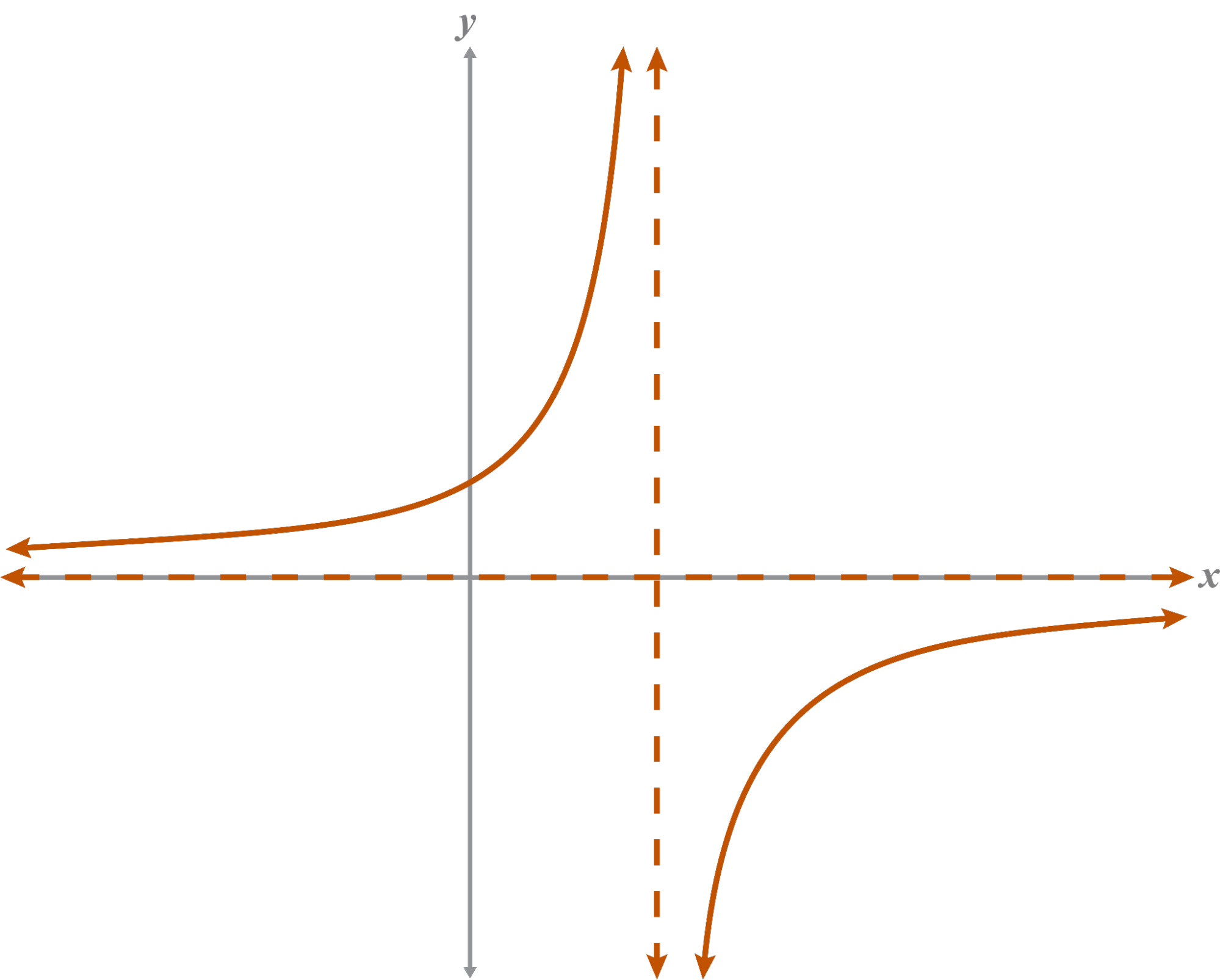
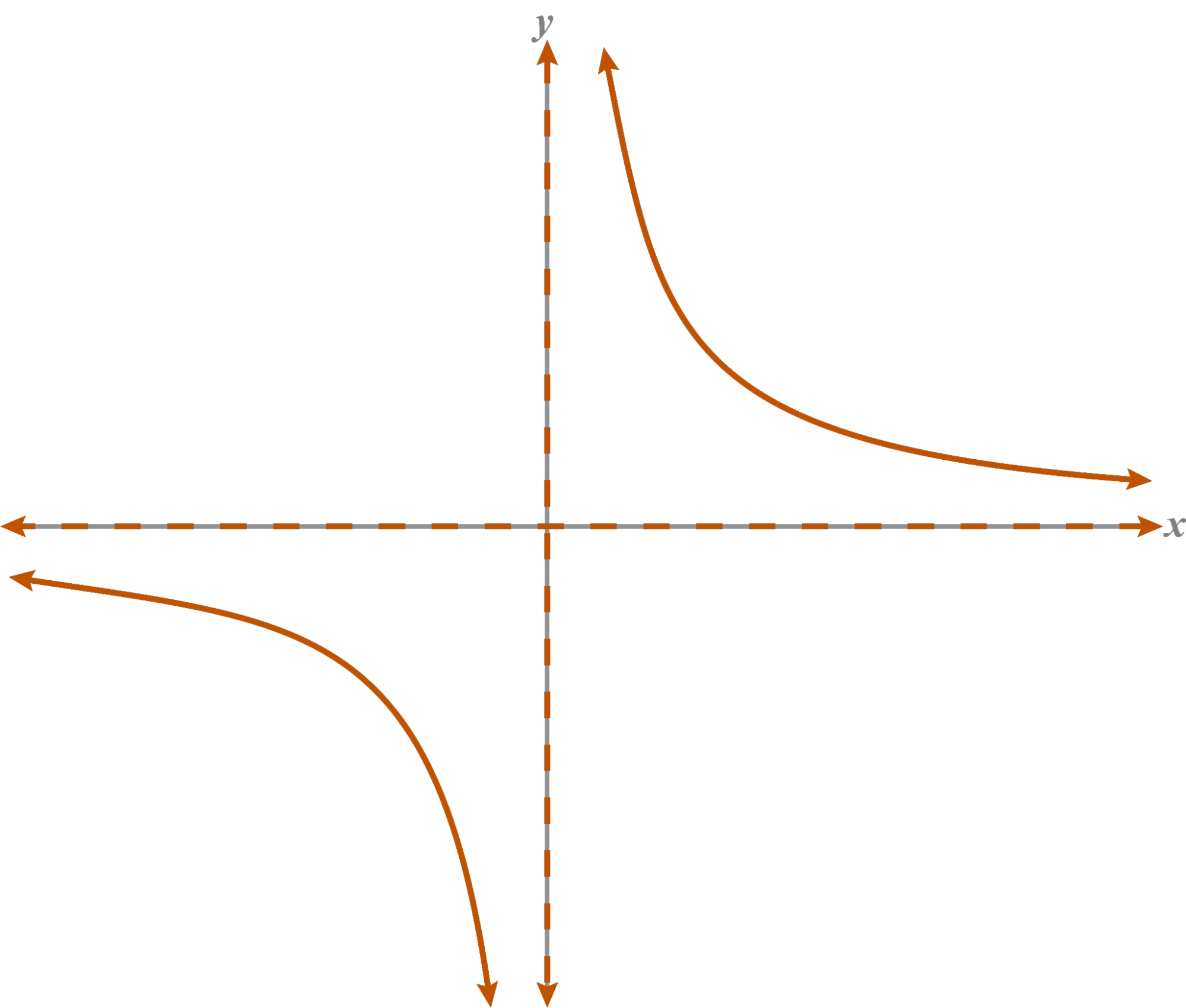
Which graph would be sketched closer to the origin? Explain.

$f (x) = \frac{1}{5 x} g (x) = \frac{1}{2 x}$

$\frac{1}{5 x}$ will be sketched closer to the origin because $\frac{1}{5}$ is less than $\frac{1}{2}$ .

Describe what the value of h does to the graph of a reciprocal function.
A positive h-value will shift the graph right h-spaces.
A negative h-value will shift the graph left h-spaces.

Name any asymptotes and intercepts from the given graph. Describe the transformation from the parent graph.

$f (x) = \frac{- 1}{4 (x + 1)} - 3$

$a = - \frac{1}{4}, h = - 1, k = - 3 \begin{matrix} \end{matrix} \begin{matrix} x ‐ intercept & y ‐ intercept \\ 0 = \frac{- 1}{4 (x + 1)} - 3 & f (0) = \frac{- 1}{4 (0 + 1)} - 3 \\ 3 = \frac{- 1}{4 (x + 1)} & = \frac{- 1}{4} - 3 \\ 12 (x + 1) = - 1 & f (0) = - 3 \frac{1}{4} \\ 12 x + 12 = - 1 \\ 12 x = - 13 \\ x = - \frac{13}{12} \end{matrix}$

Asymptotes: x = –1, y = –3
Intercept(s): $(- \frac{13}{12}, 0), (0, - 3 \frac{1}{4})$

The function is one space left and three spaces down from the parent graph because $h = - 1, k = - 3 .$ The graph is reflected and compressed vertically because $a = - \frac{1}{4}$ .

$g (x) = \frac{4}{x}$

$a = 4, h = 0, k = 0 \begin{matrix} x - intercept & y - intercept \\ none & none \end{matrix}$

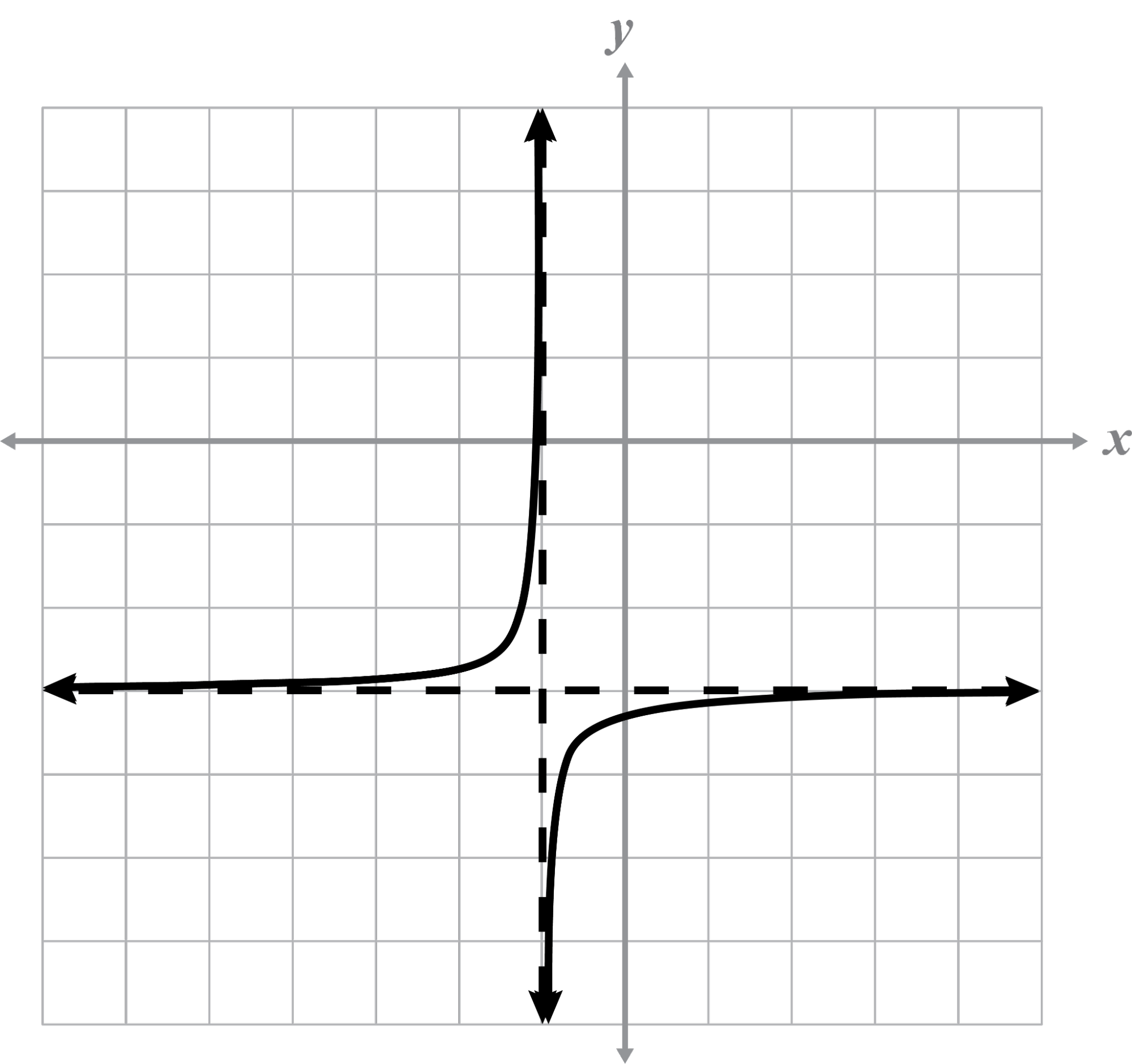
Asymptotes: x = 0, y = 0
Intercept(s): none

The function did not shift from the parent graph. The graph is stretched vertically by a factor of 4 because $a = 4 .$

$h (x) = \frac{- 3}{x - 5} + 2$

$a = - 3, h = 5, k = 2 \begin{matrix} x ‐ intercept & y ‐ intercept \\ 0 = \frac{- 3}{x - 5} + 2 & h (0) = \frac{- 3}{0 - 5} + 2 \\ - 2 = \frac{- 3}{x - 5} & = \frac{3}{5} + 2 \\ - 2 (x - 5) = - 3 & h (0) = 2 \frac{3}{5} \\ - 2 x + 10 = - 3 \\ - 2 x = - 13 \\ x = \frac{13}{2} \end{matrix}$

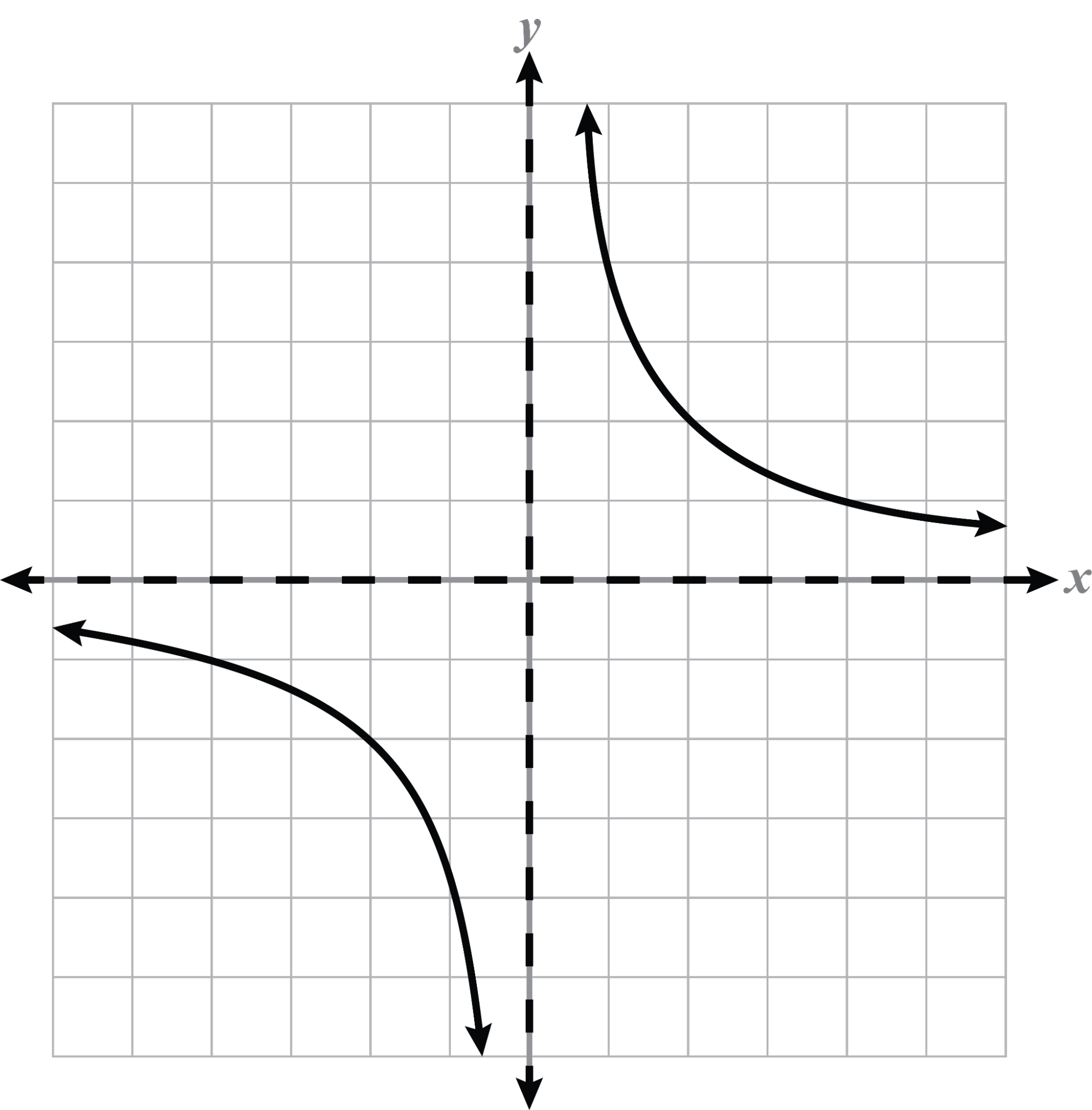
Asymptotes: x = 5, y = 2
Intercept(s): $(\frac{13}{2}, 0), (0, 2 \frac{3}{5})$
The function is five spaces to the right and two spaces up from the parent graph because $h = 5, k = 2 .$ The graph is reflected and stretched vertically because $a = - 3 .$

$j (x) = \frac{- 2}{3 (x - 2)} + 1$

$a = - \frac{2}{3}, h = 2, k = 1 \begin{matrix} x ‐ intercept & y ‐ intercept \\ 0 = \frac{- 2}{3 (x - 2)} + 1 & j (0) = \frac{- 2}{3 (0 - 2)} + 1 \\ - 1 = \frac{- 2}{3 (x - 2)} & = \frac{- 2}{3 (- 2)} + 1 \\ - 3 (x - 2) = - 2 & = \frac{1}{3} + 1 \\ - 3 x + 6 = - 2 & j (0) = 1 \frac{1}{3} \\ - 3 x = - 8 \\ x = \frac{8}{3} \end{matrix}$

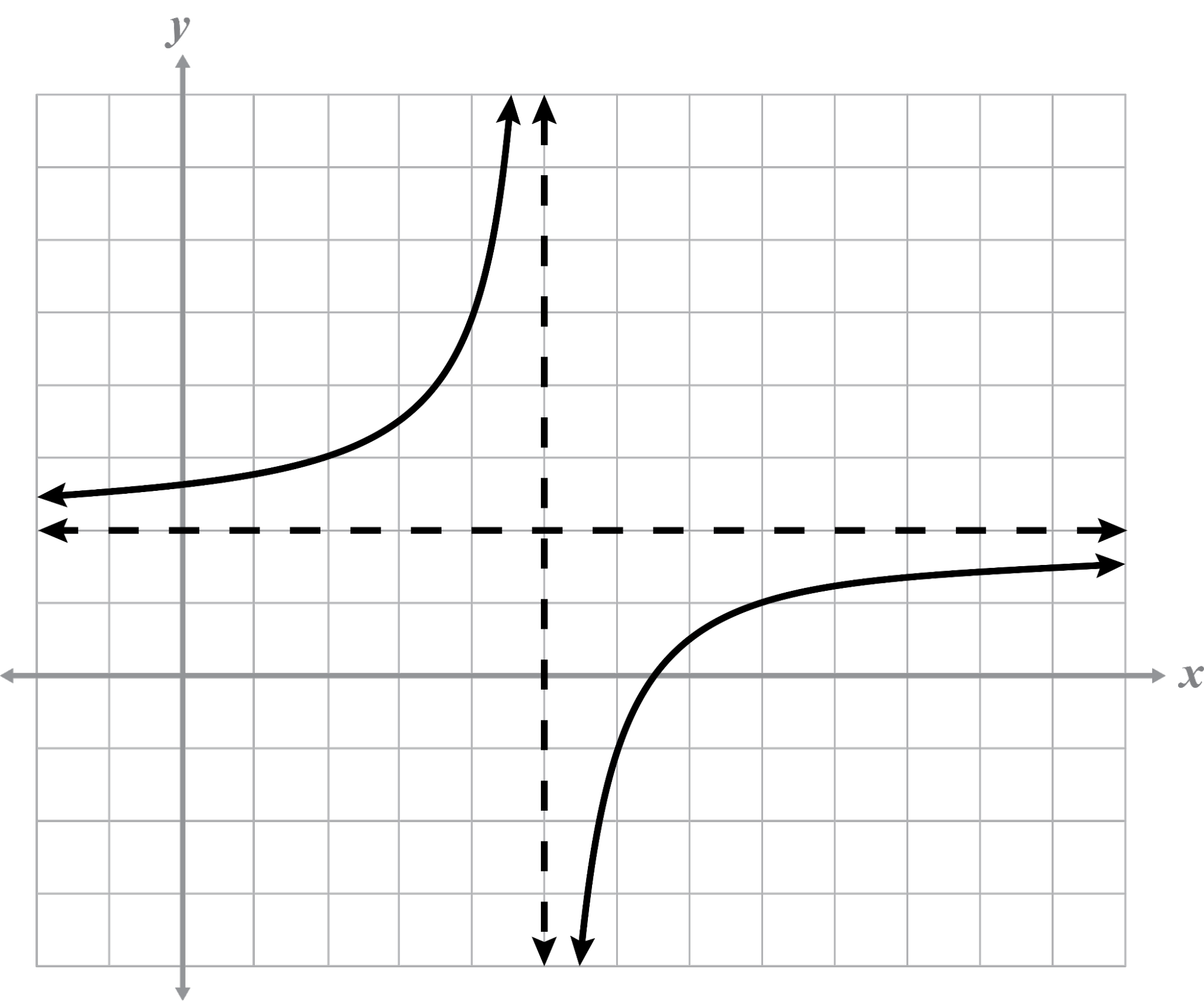
Asymptotes: x = 2, y = 1
Intercept(s): $(\frac{8}{3}, 0), (0, 1 \frac{1}{3})$

The function is two spaces to the right and one space down from the parent graph because $h = 2, k = 1 .$ The graph is reflected and compressed vertically because $a = - \frac{2}{3}$ .

$b (x) = \frac{5}{x - 3}$

$a = 5, h = 3, k = 0 \begin{matrix} x ‐ intercept & y ‐ intercept \\ none & b (0) = \frac{5}{0 - 3} \\ b (0) = - \frac{5}{3} \end{matrix}$

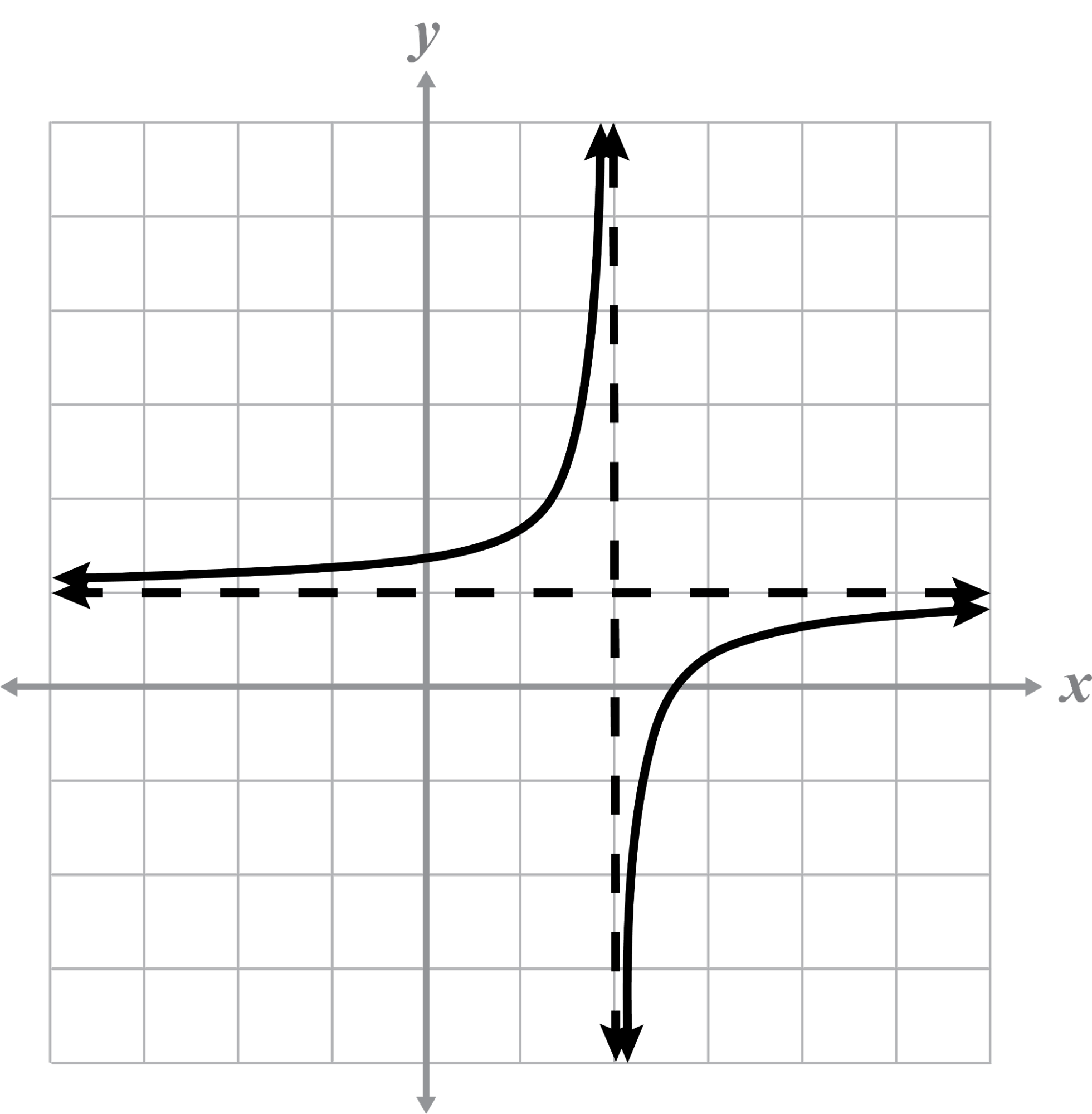
Asymptotes: x = 3, y = 0
Intercept(s): $(0, - \frac{5}{3})$

The function is three spaces to the right from the parent graph because $h = 3, k = 0 .$ The graph is stretched vertically because $a = 5 .$

$a (x) = \frac{- 4}{9 x} - 4$

$\begin{array}{rcl} a & = & - \frac{4}{9}, h = 0, k = - 4 \\ \begin{matrix} x ‐ intercept & y ‐ intercept \\ 0 = \frac{- 4}{9 x} - 4 & none \\ 4 = \frac{- 4}{9 x} 36 x = - 4 x = - \frac{1}{9} \end{matrix} \end{array}$

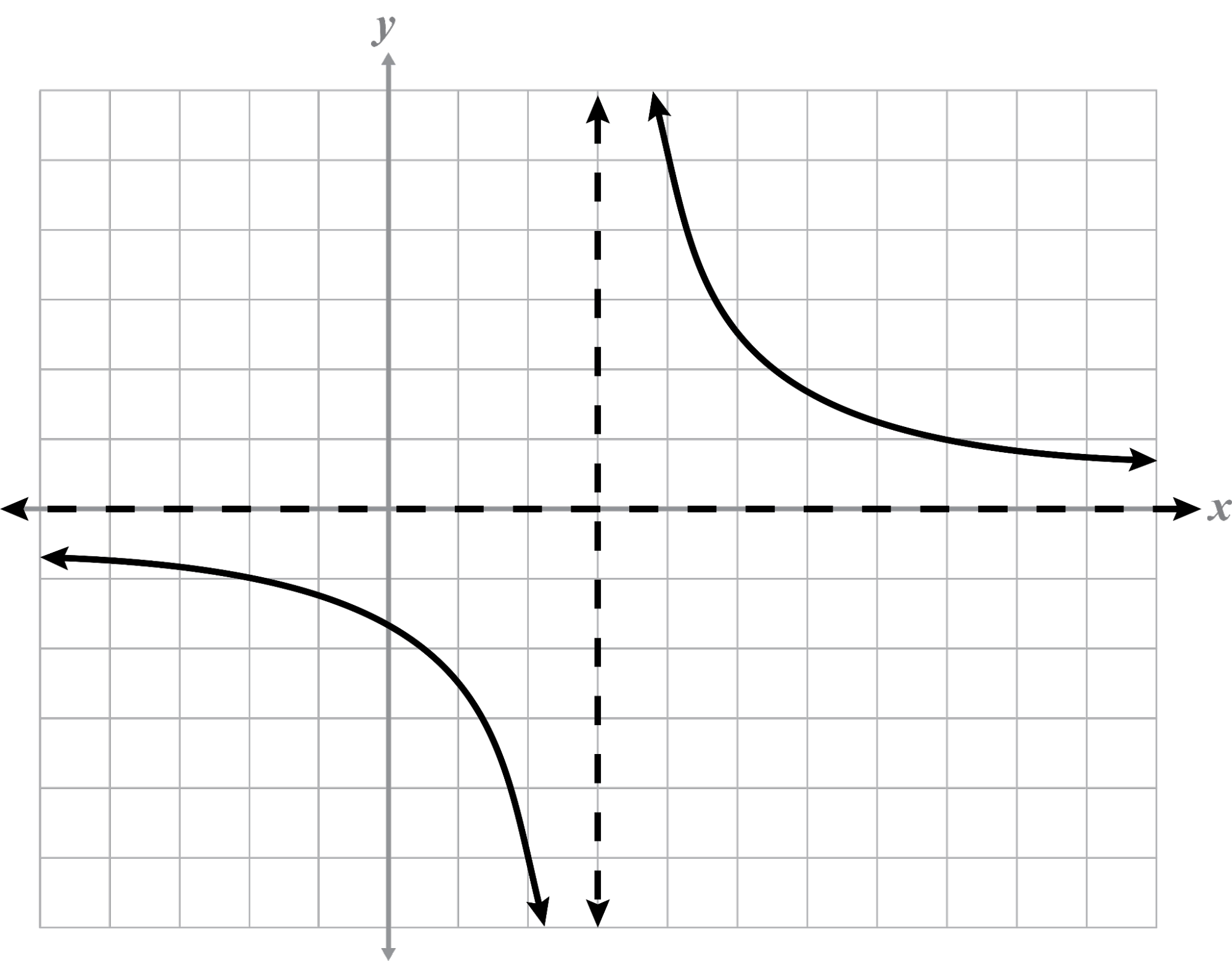
Asymptotes: x = 0, y = –4
Intercept(s): $(- \frac{1}{9}, 0)$
The function is four spaces down from the parent graph because $h = 0, k = - 4 .$ The graph is reflected and compressed vertically because $a = - \frac{4}{9}$ .

Name a, h, and k. Determine the domain and range of the reciprocal function. Graph the asymptotes. Sketch the hyperbola.

Note

The x- and y-intercepts are not plotted on the graph, but can be found algebraically or can be estimated from the graph in the Worked Solution. See More to Explore to see how technology can be used to check graphs and determine intercepts, if needed.

$g (x) = \frac{6}{x + 3} - 2$

$a = 6, h = - 3, k = - 2 Domain : \{x | x \in ℝ, x \neq - 3\} Range : \{y | y \in ℝ, y \neq - 2\}$

$f (x) = \frac{- 1}{5 x} - 8$

$a = - 1, h = 0, k = - 8 Domain : \{x | x \in ℝ, x \neq 0\} Range : \{y | y \in ℝ, y \neq - 8\}$

$h (x) = \frac{4}{x - 6} + 6$

$a = 4, h = 6, k = 6 Domain : \{x | x \in ℝ, x \neq 6\} Range : \{y | y \in ℝ, y \neq 6\}$

$b (x) = \frac{- 2}{x + 4} + 5$

$a = - 2, h = - 4, k = 5 Domain : \{x | x \in ℝ, x \neq - 4\} Range : \{y | y \in ℝ, y \neq 5\}$

$a (x) = \frac{- 5}{x - 3}$

$a = - 5, h = 3, k = 0 Domain : \{x | x \in ℝ, x \neq 3\} Range : \{y | y \in ℝ, y \neq 0\}$

$k (x) = \frac{7}{x}$

$a = 7, h = 0, k = 0 Domain : \{x | x \in ℝ, x \neq 0\} Range : \{y | y \in ℝ, y \neq 0\}$