Explore
Transformations on the Coordinate Plane Solutions
-
- The Coordinate Plane is made up by a horizontal number line, the x-axis , and a vertical number line, the y-axis .
- Each coordinate represents a point on the coordinate plane.
- A reflection is a mirror image after a shape or graph has been flipped over the line of reflection.
- A translation is a shift , either horizontal, vertical, or both, on the coordinate plane.
To reflect a figure over the x-axis:
-
- Label each vertex as .
- Each point will become in the reflected image.
To reflect a figure over the y-axis:
-
- Label each vertex as .
- Each point will become in the reflected image.
To translate a point horizontally:
-
- Subtract the horizontal translation from the x -coordinate to move the point to the left.
- Add the horizontal translation to the x -coordinate to move the point to the right.
To translate a point vertically:
-
-
Subtract the vertical translation from the y -coordinate to move the point down .
-
Add the vertical translation to the y -coordinate to move the point up .
- To translate a figure, translate each vertex based on the given translation.
Example 1
Reflect or translate the coordinate on the graph.
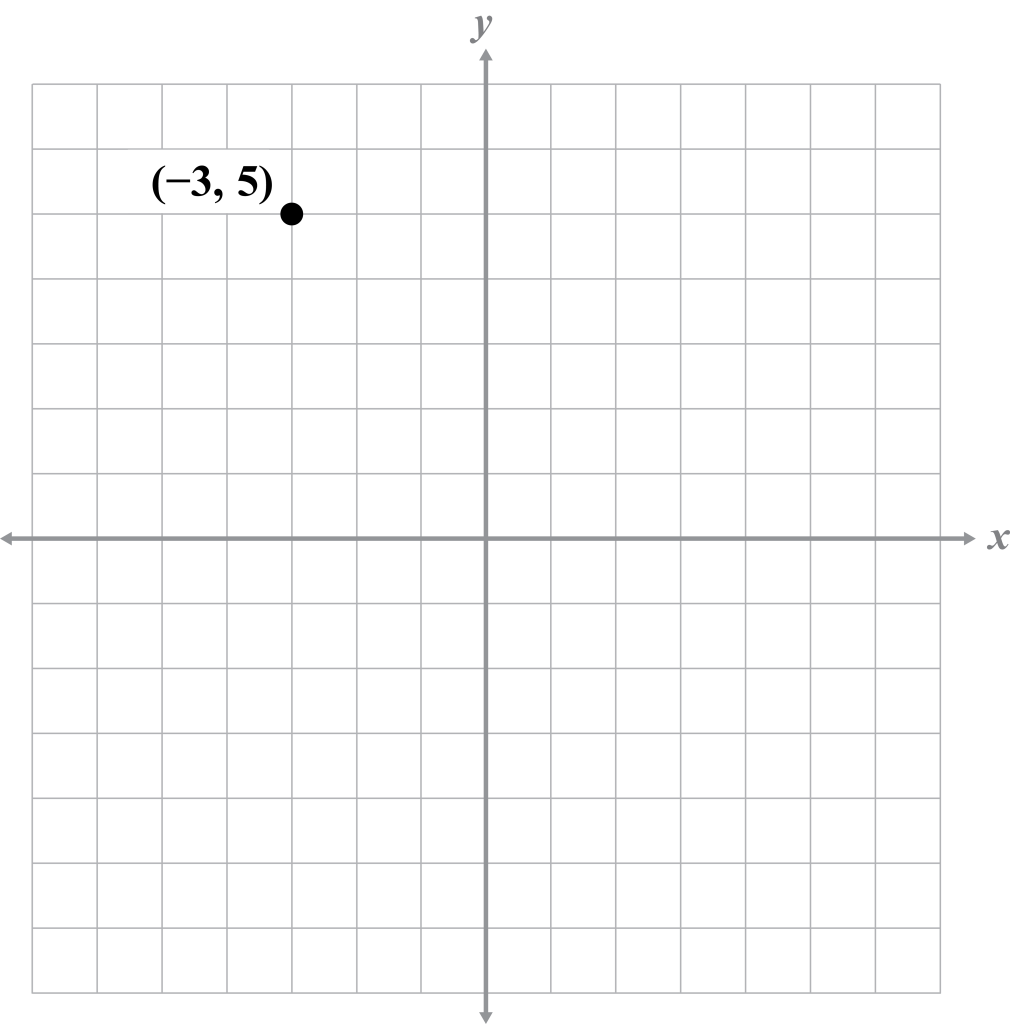
- Reflect over the x-axis.
Plan
- Translate right two units, down eight units.
Plan
Translate right: add 2 units to x-coordinate.
Translate down: subtract 8 units from y-coordinate.
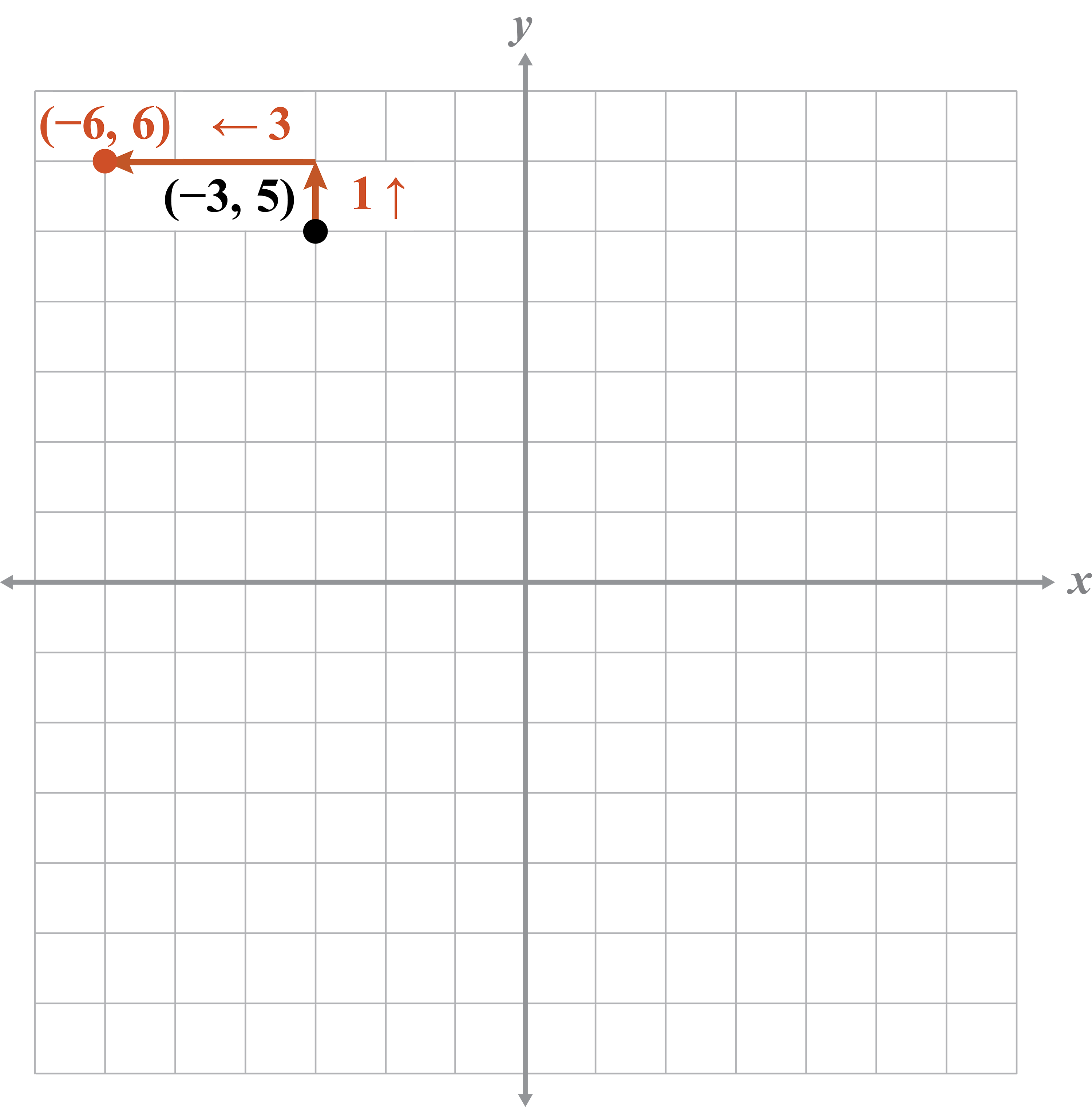
- Translate left three units, up one unit.
Plan
Translate left: subtract 3 units from x-coordinate.
Translate up: add 1 unit to y-coordinate.
Example 2
Reflect the figure over the given axis.
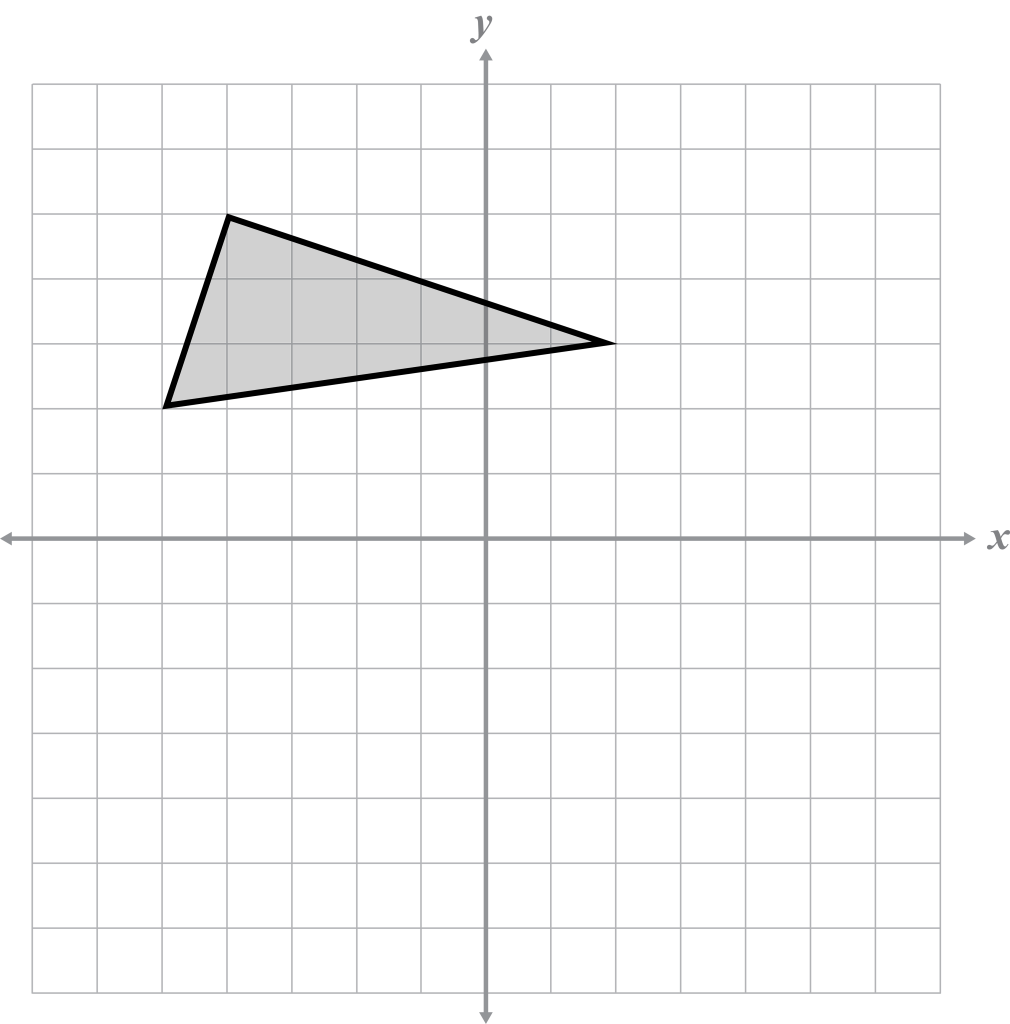
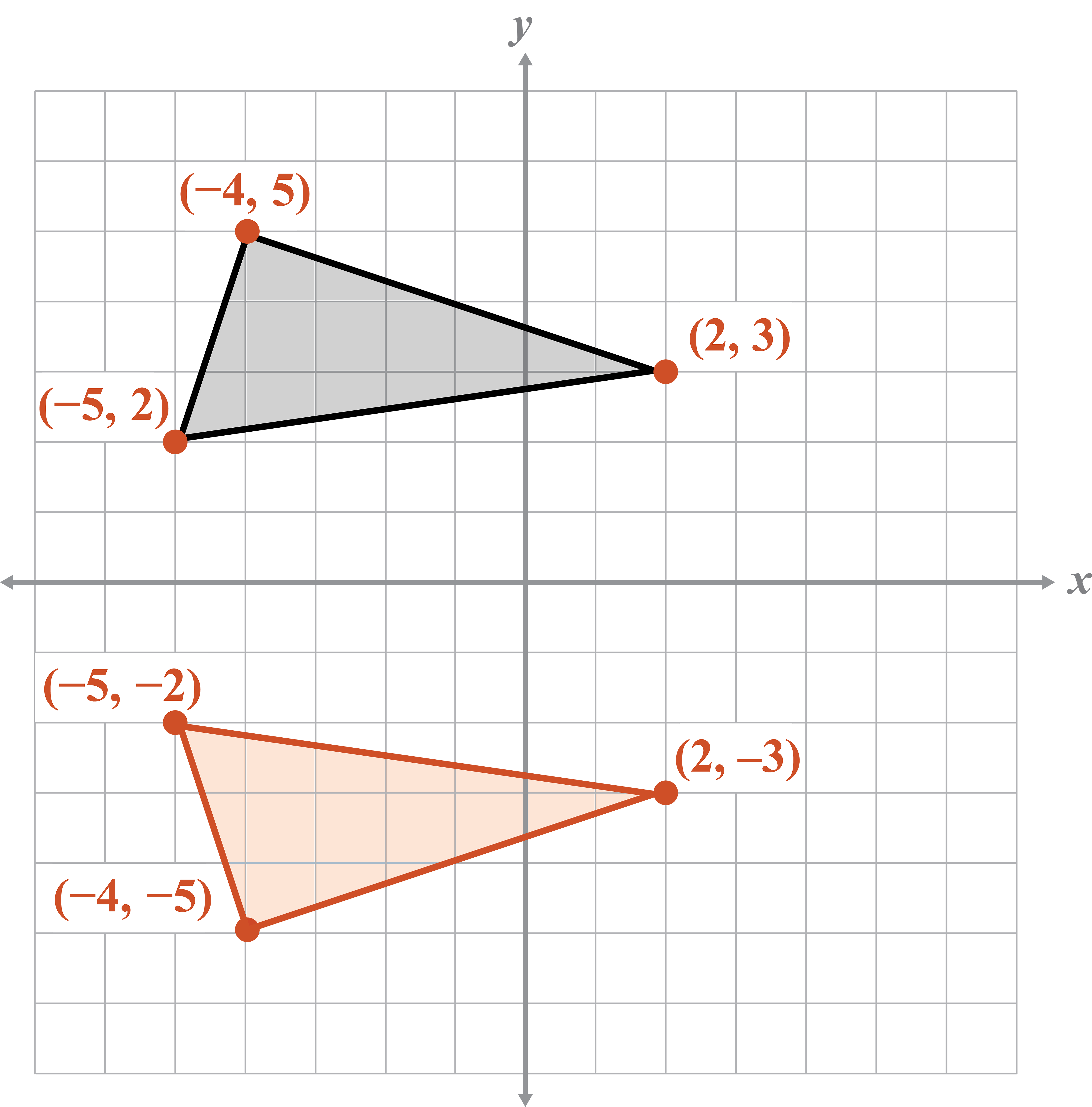
- Reflect the figure over the x-axis.
Plan
Label each vertex .
Plot the reflected points .
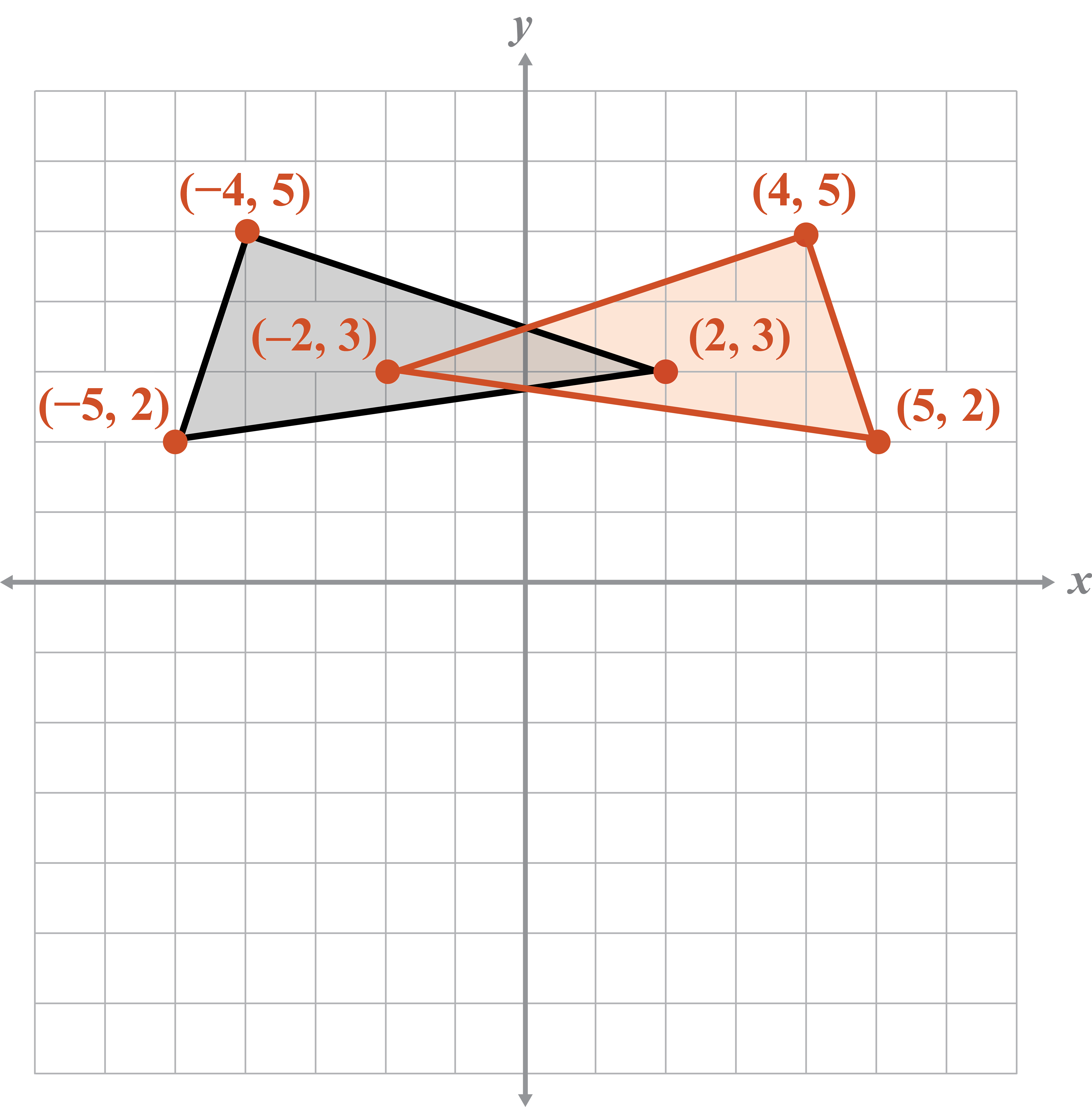
- Reflect the figure over the y-axis.
Plan
Label each vertex
Plot the reflected points
Example 3
Translate the figure.
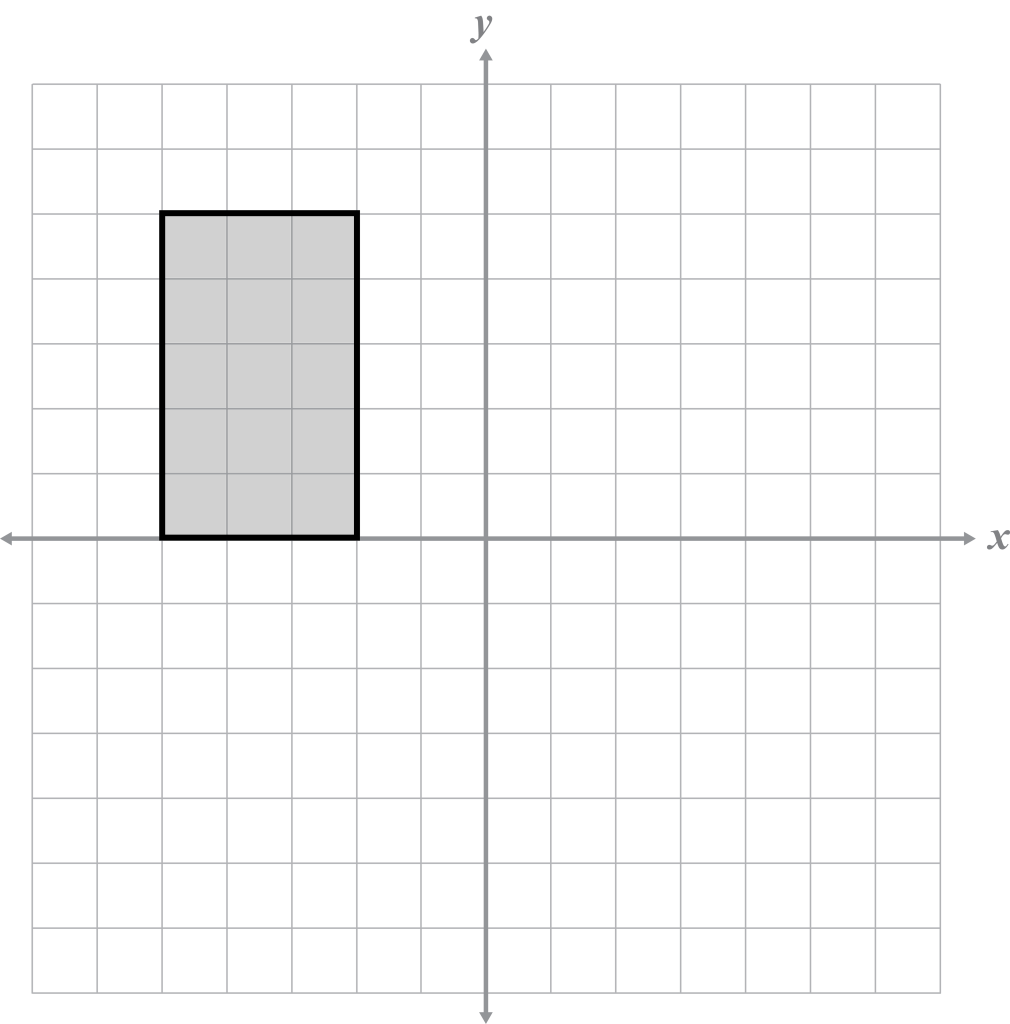
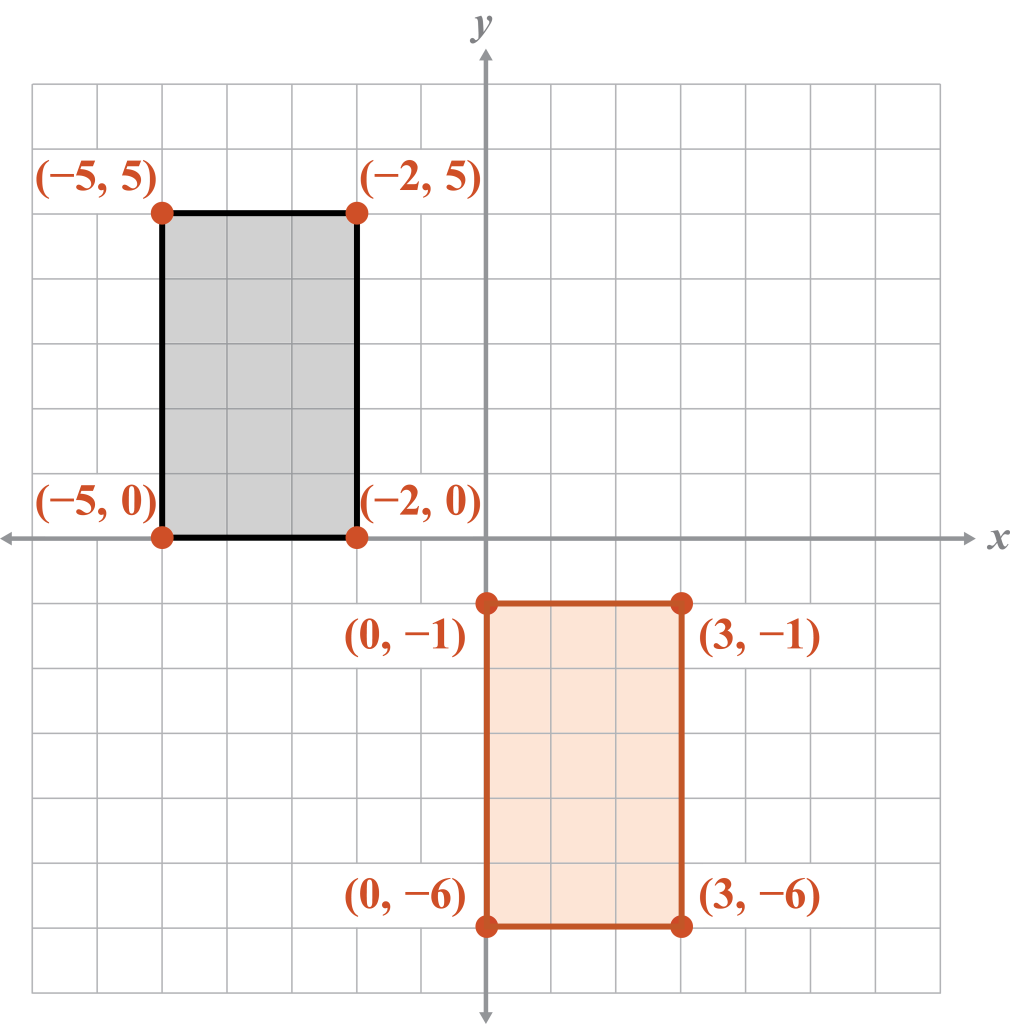
Translate 5 units right and 6 units down.
Plan
Label each vertex
Shift each vertex