Targeted Review Solutions

Solve: $- {(x + 8)}^{2} = 24$

$\begin{array}{rcl} {(x + 8)}^{2} & = & - 24 \\ \sqrt{{(x + 8)}^{2}} & = & \pm \sqrt{- 24} \\ x + 8 & = & \pm 2 i \sqrt{6} \end{array}$

$\begin{array}{rcl} x & = & - 8 \pm 2 i \sqrt{6} \end{array}$

Solve: $7 x^{3} = - 56 x$

$\begin{array}{rcl} 7 x^{2} + 56 x & = & 0 \\ 7 x (x^{2} + 8) & = & 0 \\ \begin{matrix} 7 x = 0 & x^{2} + 8 = 0 \\ x = 0 & x^{2} = - 8 \\ \sqrt{x^{2}} = \pm \sqrt{- 8} \\ x = \pm 2 i \sqrt{2} \end{matrix} \end{array}$

$x = \pm 2 i \sqrt{2}, 0$

Write the polynomial equation with integer coefficients given the roots: $x = \sqrt{3}, \pm 2 i$

$x = - \sqrt{3}, x = \sqrt{3}, x = - 2 i, x = 2 i (x + \sqrt{3}) (x - \sqrt{3}) (x + 2 i) (x - 2 i) = 0 (x^{2} - 3) (x^{2} - 4 i^{2}) = 0 (x^{2} - 3) (x^{2} - 4 (- 1)) = 0 (x^{2} - 3) (x^{2} + 4) = 0 x^{4} + 4 x^{2} - 3 x^{2} - 12 = 0$

$x^{4} + x^{2} - 12 = 0$

Calculate the discriminant for the equation $y = - 5 x^{2} - x - 0.2$ . Explain what this tells you about the roots.

$a = - 5, b = - 1, c = - 0.2 b^{2} - 4 a c {(- 1)}^{2} - 4 (- 5) (- 0.2) 1 - 4 - 3$

A discriminant of –3 means the equation has zero real roots. Another way of saying it is that the equation has two complex roots.

Problems 5–7 work together.

Graph.
$y = - 2 {(x - 1)}^{2} + 1 y = 2 x - 5$

$parabola : a = - 2, (1, 1) line : m = 2, b = - 5$

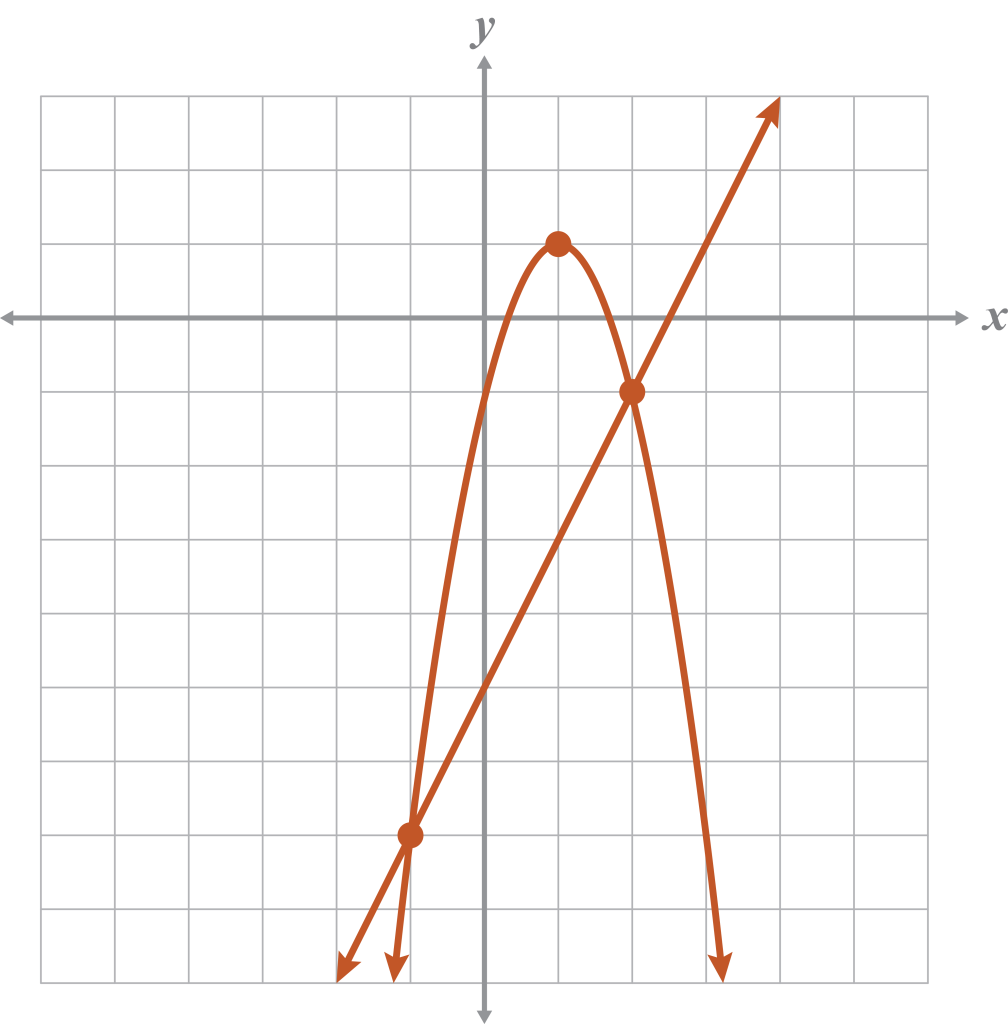
Using your graph from problem 5, calculate the midpoint of the line segment inside the parabola using the points of intersection. Use the intersection points to calculate the midpoint of the line segment inside the parabola.

$(- 1, - 7), (2, - 1) (\frac{- 1 + 2}{2}, \frac{- 7 + - 1}{2})$

$(\frac{1}{2}, - 4)$

Using your work for problems 5 and 6, calculate the distance between the vertex and midpoint of the line segment. Write the answer in radical form.

$(1, 1), (\frac{1}{2}, - 4) d = \sqrt{{(1 - \frac{1}{2})}^{2} + {(1 - (- 4))}^{2}} d = \sqrt{{(\frac{1}{2})}^{2} + {(5)}^{2}} = \sqrt{25 \frac{1}{4}} d = \sqrt{\frac{101}{4}} = \frac{\sqrt{101}}{\sqrt{4}}$

$d = \frac{\sqrt{101}}{2}$

Solve $8 x^{2} - 5 x = 0$ using the quadratic formula.

$a = 8, b = - 5, c = 0 x = \frac{- (- 5) \pm \sqrt{{(- 5)}^{2} - 4 (8) (0)}}{2 (8)} x = \frac{5 \pm \sqrt{25 - 0}}{16} = \frac{5 \pm 5}{16} x = \frac{10}{16}, \frac{0}{16}$

$x = 0, \frac{5}{8}$

Multiple Choice

Determine the value of b to form a perfect square trinomial: $x^{2} + b x + \frac{4}{25}$

$- \frac{4}{5}$
$\frac{4}{5}$
$\frac{2}{5}$
$\frac{4}{625}$

$a = 1, c = \frac{4}{25} b = 2 \sqrt{a c} b = 2 \sqrt{\frac{4}{25}} = 2 (\frac{2}{5}) b = \frac{4}{5}$

Note

This value is the opposite of the solution.
This value is the square root of (ac) but does not multiply it by 2.
This value would occur if solving for c rather than b.

Right triangle ABC is graphed on the coordinate plane. Determine the length of the hypotenuse, AC, when $A (- 7, 10), B (8, 4)$ , and $C (4, - 6)$ .

$3 \sqrt{29}$
$2 \sqrt{29}$
$\sqrt{377}$
5

$(- 7, 10), (4, - 6) A C = \sqrt{{(- 7 - 4)}^{2} + {(10 + 6)}^{2}} A C = \sqrt{{(- 11)}^{2} + {(16)}^{2}} = \sqrt{121 + 256} A C = \sqrt{377}$

Note

This solution is the distance of segment AB.
This solution is the distance of segment BC.
This error occurs if subtraction is not used in the distance formula.

Determine the polynomial equation given the roots: 3i, 5i.

$x^{2} + 2 i x + 15 = 0$
$x^{4} + 34 x^{2} + 225 = 0$
$x^{3} + 5 i x^{2} + 9 x + 45 i = 0$
$x^{4} - 34 x^{2} + 225 = 0$

$x = \pm 3 i, \pm 5 i (x - 3 i) (x + 3 i) (x - 5 i) (x + 5 i) = 0 (x^{2} - 9 i^{2}) (x^{2} - 25 i^{2}) = 0 (x^{2} + 9) (x^{2} + 25) = 0 x^{4} + 25 x^{2} + 9 x^{2} + 225 = 0 x^{4} + 34 x^{2} + 225 = 0$

Note

This answer does not include the roots –3i and –5i.
This answer does not include the root –5i.
This answer is the product of the difference of squares rather than the sum of squares.

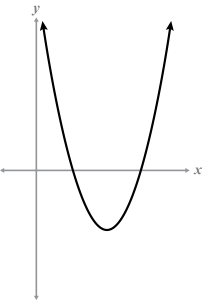
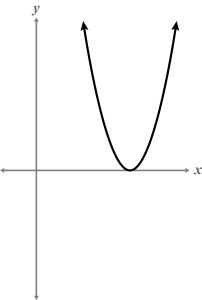
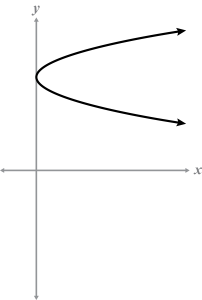
Select the graph that represents a discriminant value of zero.

$Two real roots : b^{2} - 4 a c > 0 One real root : b^{2} - 4 a c = 0 Two complex roots : b^{2} - 4 a c < 0$

Note

A, B, D) A discriminant with a value of zero intersects the x-axis at one point.

Problem	1	2	3	4	5	6	7	8	9	10	11	12
Origin	L23	L23	L23	L25	L18	L26	L26	L25	L24	L26	L23	L25

L = Lesson in this level, A1 = Algebra 1: Principles of Secondary Mathematics, FD = Foundational Knowledge