A2 Lesson 27 Explore: Writing Quadratic Equations in Vertex Form to Graph Solutions

Writing Quadratic Equations in Vertex Form to Graph Solutions

It is more efficient to graph quadratic equations in vertex form than in standard form. 
For quadratic equations that are not in vertex form, use the completing the square method to rewrite the equation in vertex form.

Quadratic Equation	Rewrite Using Completing the Square
$y = a x^{2} + b x + c \begin{matrix} or & x = a y^{2} + b y + c \end{matrix} a x^{2} + b x + c = 0 \begin{matrix} or & a y^{2} + b y + c = 0 \end{matrix} y = a {(x - h)}^{2} + k \begin{matrix} or & x = a {(y - k)}^{2} + h \end{matrix}$	Write the equation in standard form Set the equation equal to zero Complete the square to write in vertex form

Factor out a from the expression rather than dividing all terms by the leading coefficient a. 
You need to know the value of a to determine if the graph is reflected and/or dilated and the direction the parabola opens.
 To maintain equality, you must do the same thing to both sides of the equation.

Example 2

Write the quadratic equation in vertex form. Name the vertex and the axis of symmetry. Then graph.

$x - 19 + 12 y = 2 y^{2}$

Plan

Isolate x because y is the squared term 

Complete the square 

Write equation in vertex form

 Identify vertex, axis of symmetry

Graph

Implement

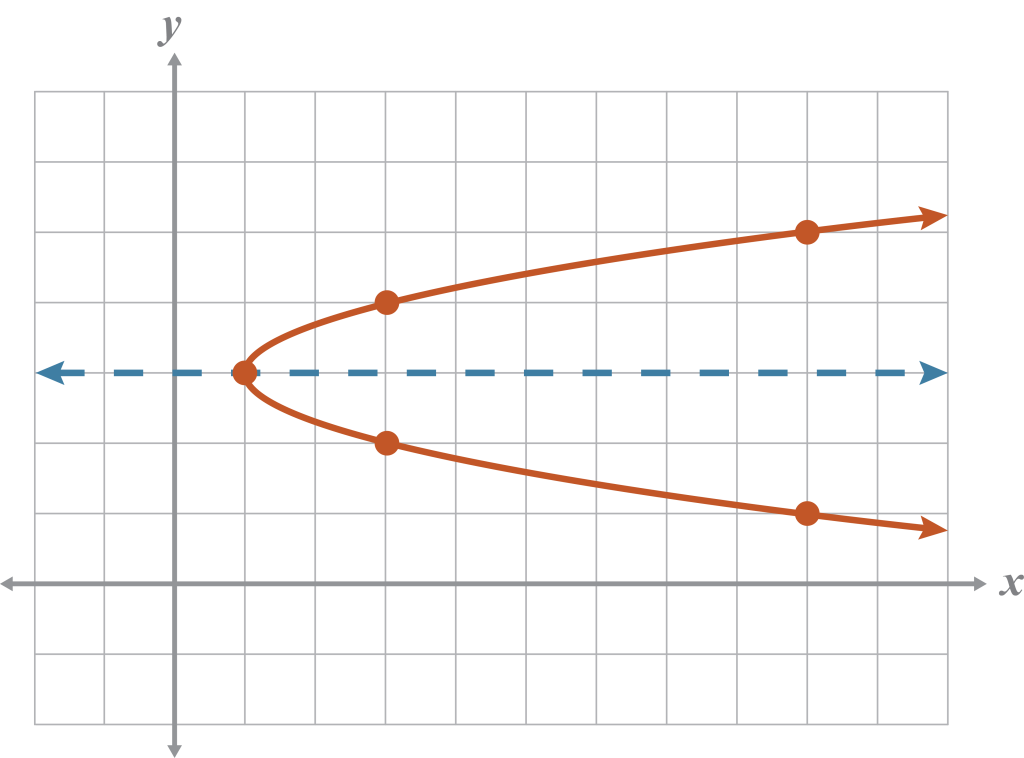
$\begin{array}{rcl} x & = & 2 y^{2} - 12 y + 19 \\ 2 y^{2} - 12 y + 19 & = & 0 \\ 2 (y^{2} - 6 y) & = & - 19 \\ 2 (y^{2} - 6 y +) & = & - 19 + 2 () \end{array}$

$\begin{array}{rcl} 2 (y^{2} - 6 y + {(\frac{- 6}{2})}^{2}) & = & - 19 + 2 ({(\frac{- 6}{2})}^{2}) \\ 2 {(y - 3)}^{2} & = & - 19 + 2 {(- 3)}^{2} \\ 2 {(y - 3)}^{2} & = & - 19 + 18 \\ 2 {(y - 3)}^{2} & = & - 1 \\ 2 {(y - 3)}^{2} + 1 & = & 0 \\ x & = & 2 {(y - 3)}^{2} + 1 \end{array}$

Explain

Isolate x, then set equation equal to zero 
Complete the square 
Recall you must do the same thing to both sides of the equation

The vertex of the parabola is $(1, 3)$ . The axis of symmetry is $y = 3$ .

Example 3

Write the quadratic equation in vertex form. Name the vertex and the axis of symmetry.

$y + 3 x = x^{2} + 2$

$y = x^{2} - 3 x + 2$

$\begin{array}{rcl} x^{2} - 3 x + 2 & = & 0 \\ x^{2} - 3 x & = & - 2 \\ (x^{2} - 3 x + {(- \frac{3}{2})}^{2}) & = & - 2 + {(- \frac{3}{2})}^{2} \\ {(x - \frac{3}{2})}^{2} & = & - \frac{8}{4} + \frac{9}{4} \\ {(x - \frac{3}{2})}^{2} & = & \frac{1}{4} \\ {(x - \frac{3}{2})}^{2} - \frac{1}{4} & = & 0 \\ y & = & {(x - \frac{3}{2})}^{2} - \frac{1}{4} \end{array}$

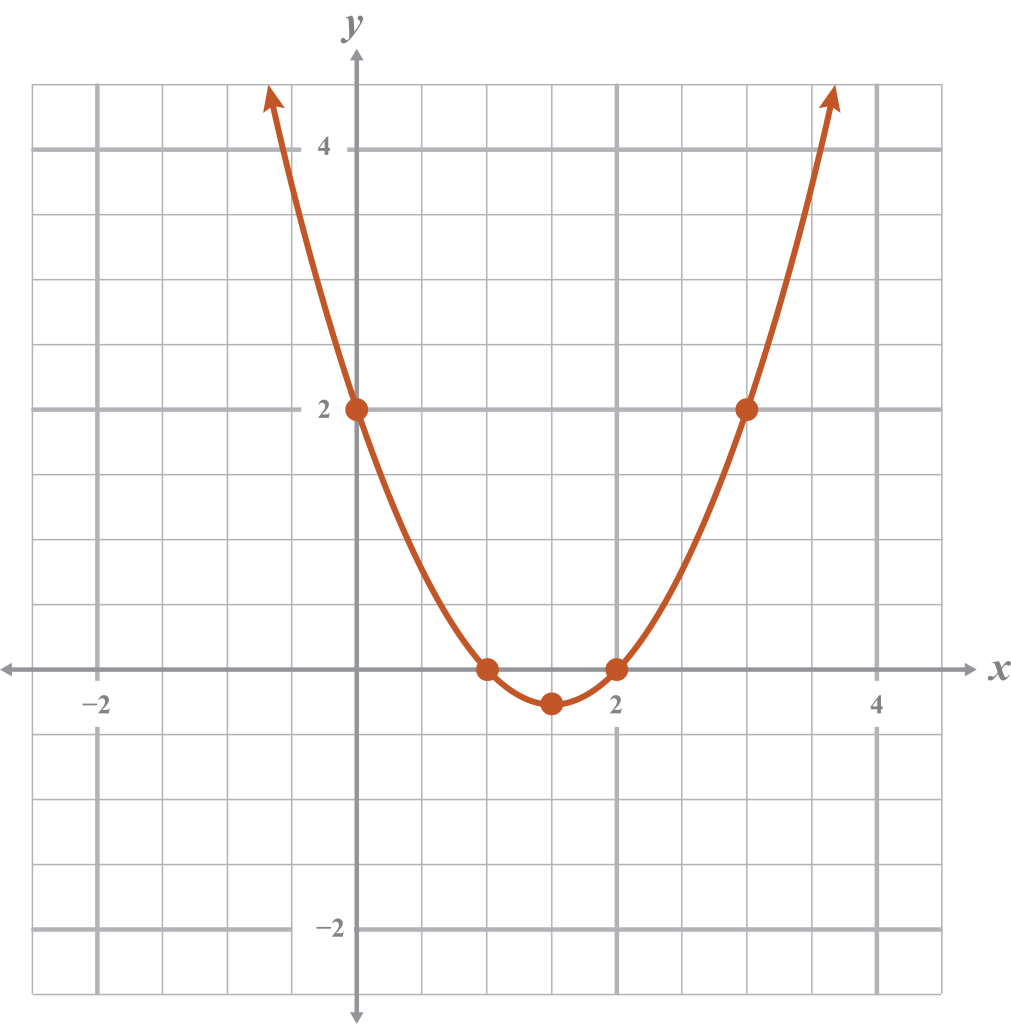
The vertex is $(\frac{3}{2}, - \frac{1}{4})$ and the axis of symmetry is $x = \frac{3}{2}$ .

Note

You could factor this equation; however, factoring would not provide all the information needed to write the equation in vertex form.

Example 4

Graph.

$0.5 y^{2} + x = - 3 y - 0.5$

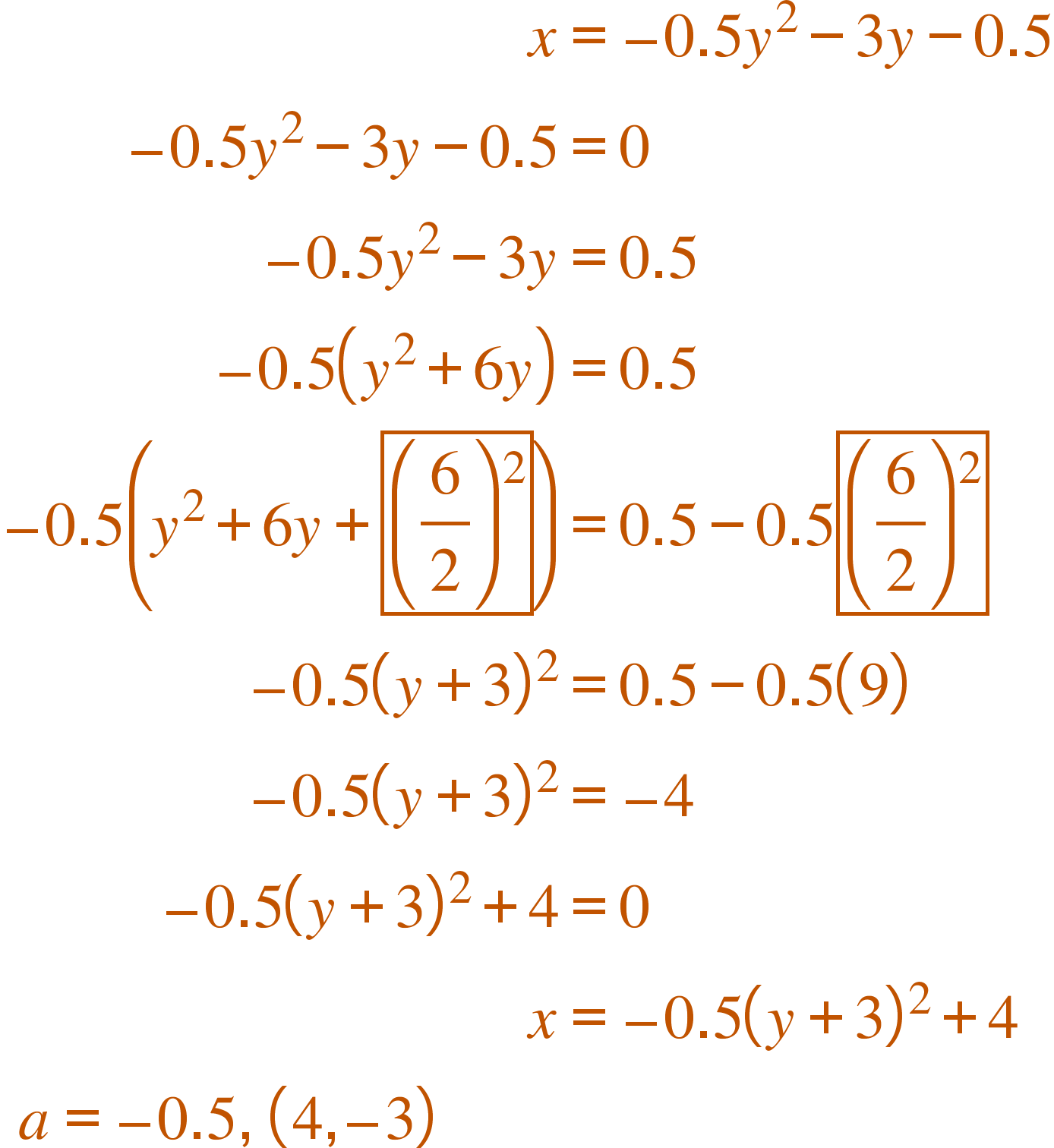
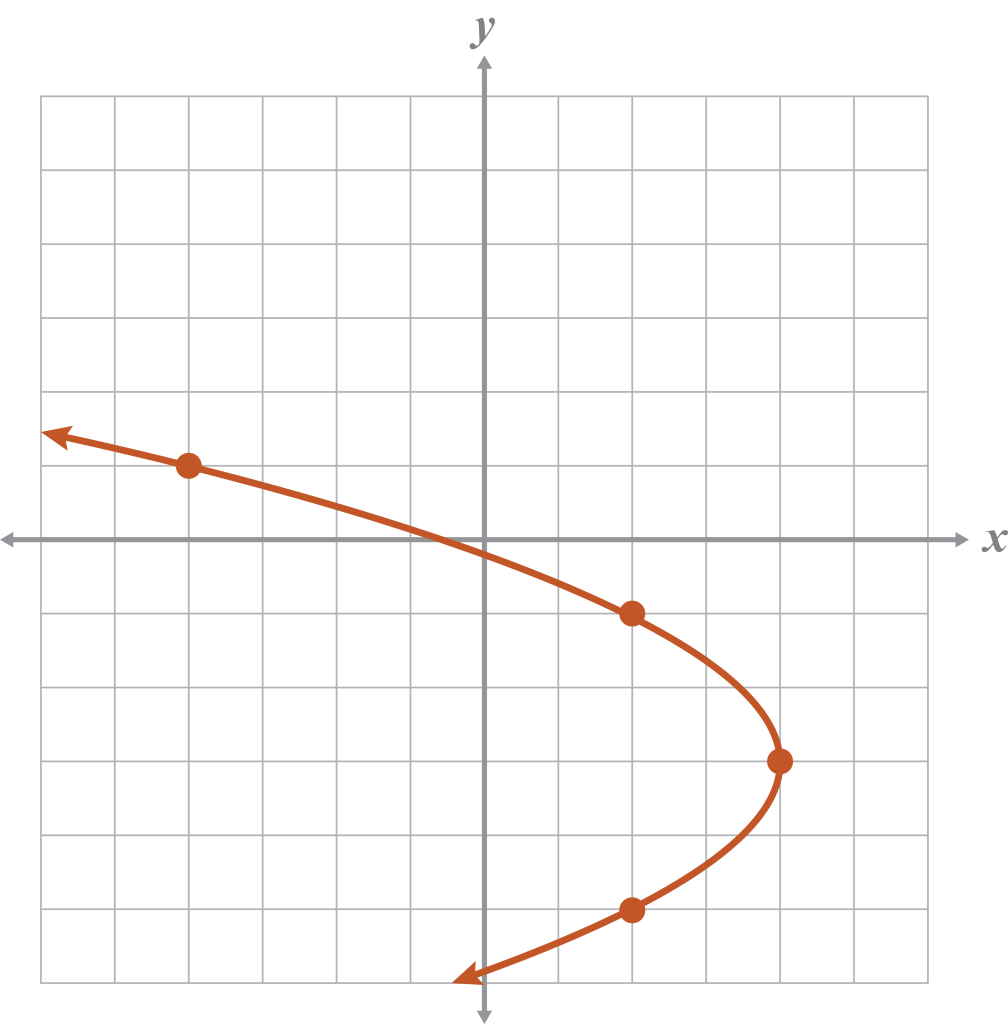
Example 5

The Dowell family has a new puppy and is fencing in a portion of their yard. They want to maximize the area by using all of the 100 feet of fencing they purchased. The fence will be used on three sides, and the fourth side will be the wall of the house. What are the dimensions and area of the fenced in space?

Plan

Identify key information and formulas 

Determine the vertex

Four sides: $P = 2 l + 2 w$

Three sides: $P = l + 2 w$

Implement

$100 = l + 2 w 100 = l + 2 w l = - 2 w + 100 A = l w A = w (- 2 w + 100) - 2 w^{2} + 100 w = 0 - 2 (w^{2} - 50 w + {(- \frac{50}{2})}^{2}) = 0 + - 2 {(- \frac{50}{2})}^{2} - 2 {(w - 25)}^{2} = - 2 (625) A = - 2 {(w - 25)}^{2} + 1250 Vertex : (25, 1250)$

$w = 25 l = - 2 (25) + 100 l = 50$

Explain

The dimensions of the fence are 50 feet by 25 feet with a maximum area of 1250 square feet.