Practice 2 Solutions
- Write the inequality for the given graph.
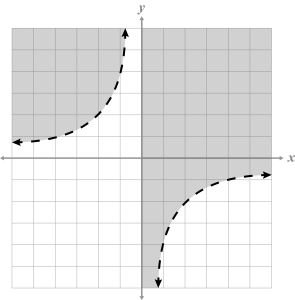
- Determine if are solutions to the graph in problem 1.
Sample: Points A and D are solutions. B is on the dashed curve; therefore it is not a solution. Point C is not a solution because it is not in the shaded region.
- Graph.
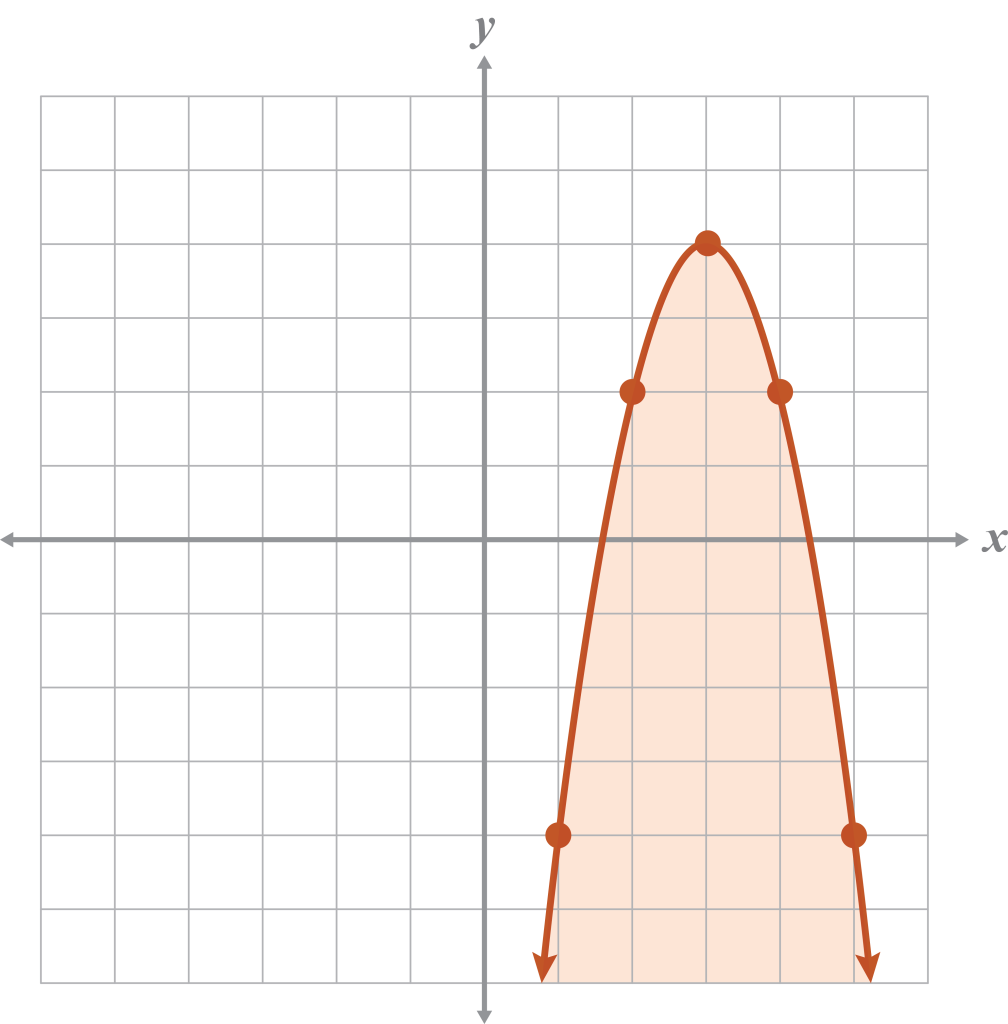
- Graph the system of inequalities and determine the solutions.
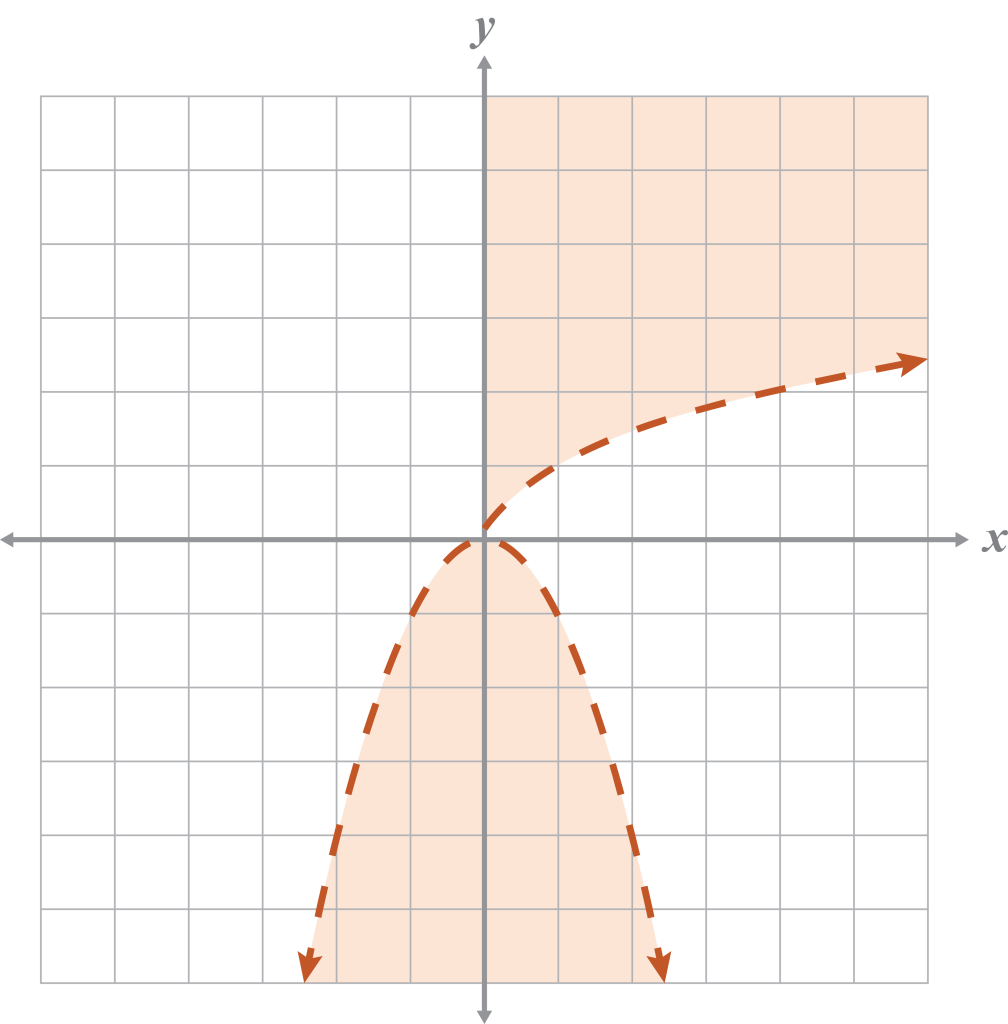
No solution
- In which quadrant(s) would the solution be located for the quadratic inequality in problem 4 if
Quadrant I
- Write the system of inequalities from the given graph.
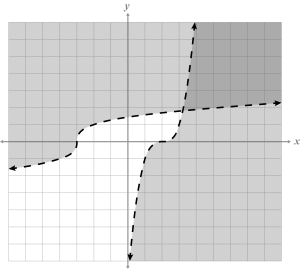
For problems 7–9, use these inequalities:
- Graph the system of inequalities.
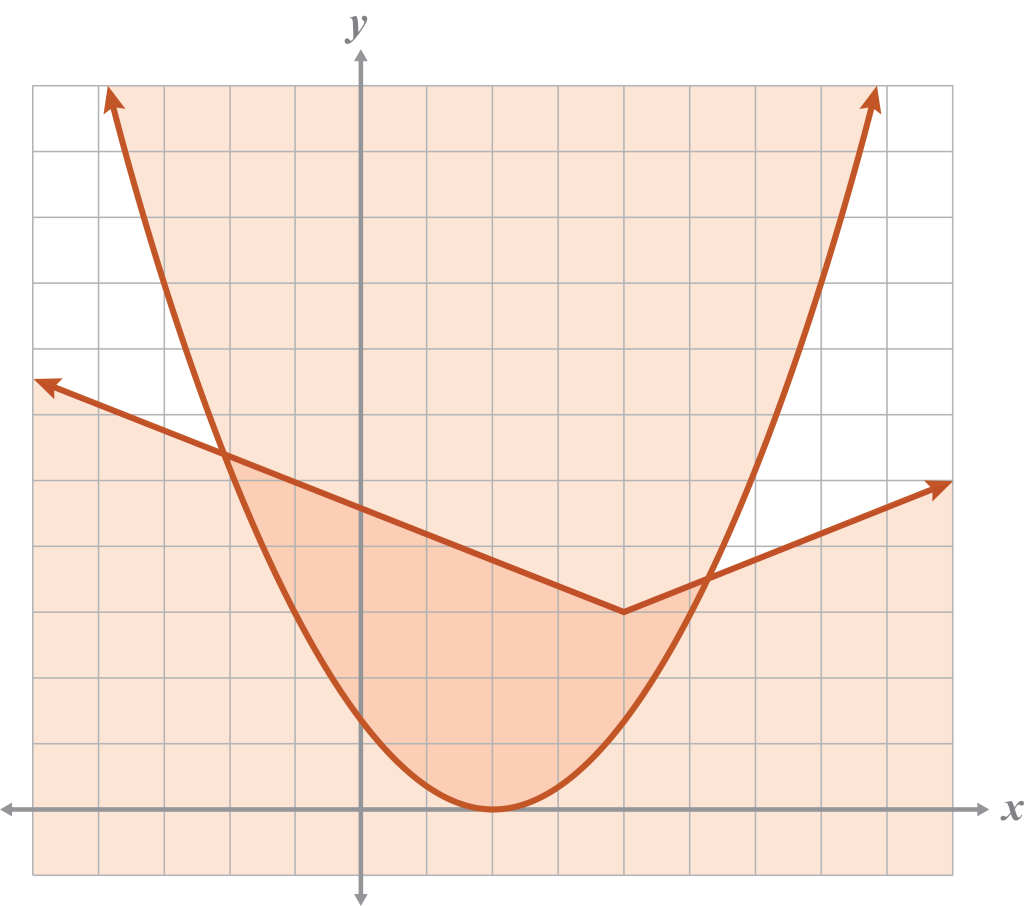
- Explain how the graph of the system would change when the absolute value inequality is
Sample: The absolute value graph would open down and the shading would be below the vertex (or inside of the v-shaped graph). The shading still intersects the current shading of the parabola and is an enclosed region for the solutions.
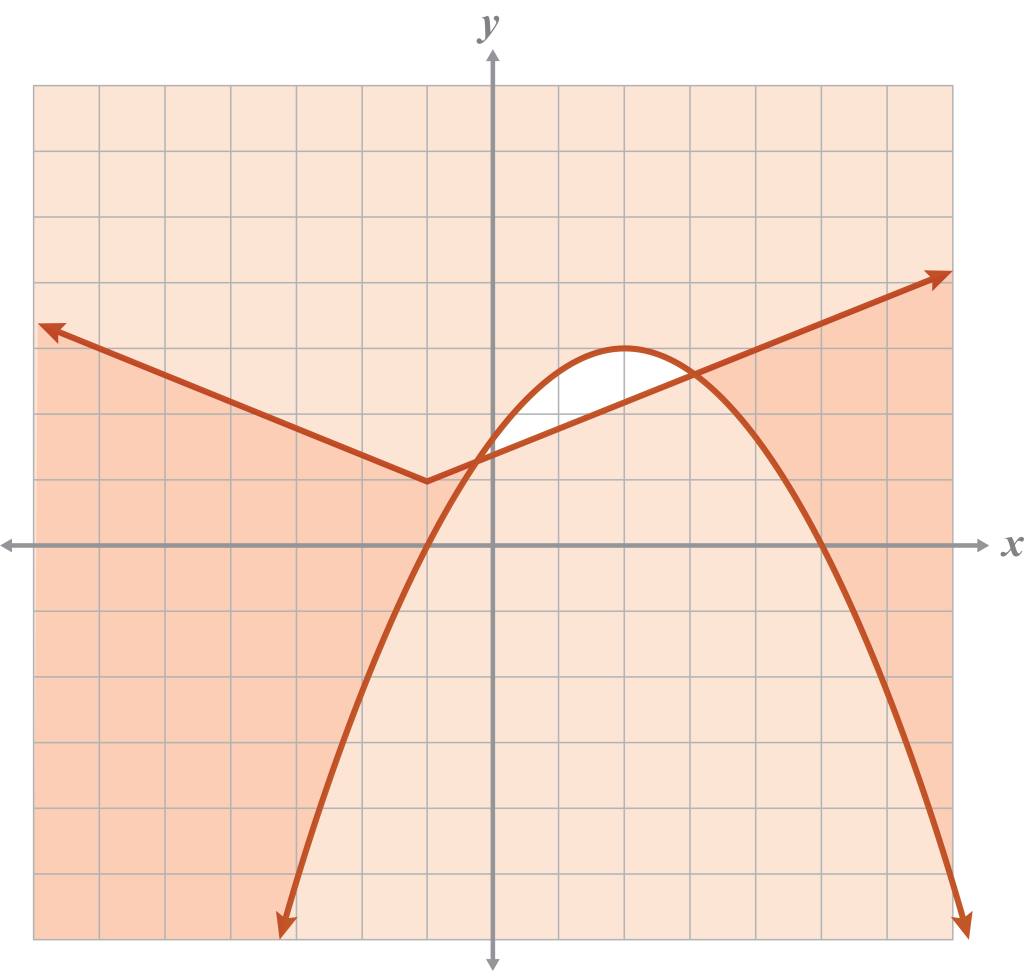
- Transform the system of inequalities in problem 7.
Translate the absolute value inequality 5 spaces to the left and down 2 spaces.
Reflect the quadratic inequality across the x-axis and translate it up 3 spaces.
- Graph the system of inequalities from problem 9.
- Graph the system of inequalities.
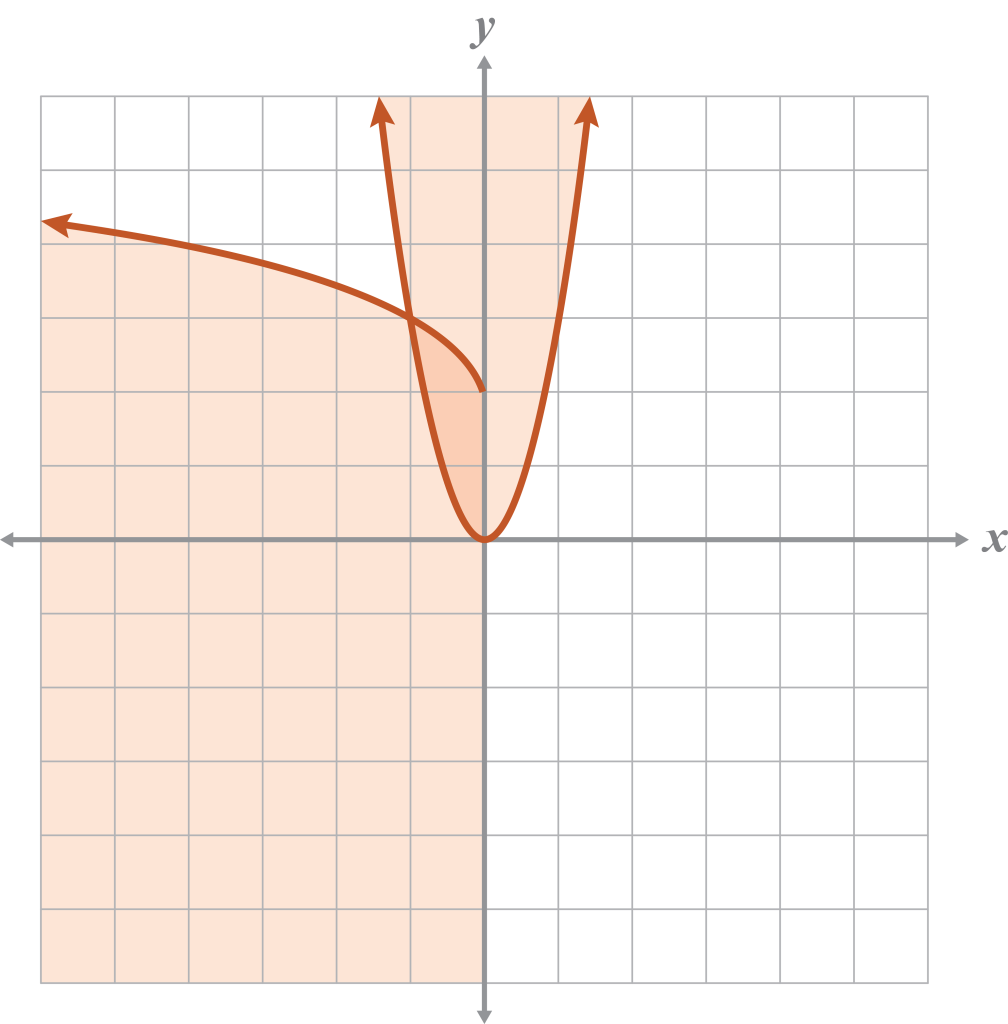
- Describe the solution if the parabola in problem 11 was translated 2 spaces to the right.
Sample: There would be no solution because the shaded regions would no longer overlap.
