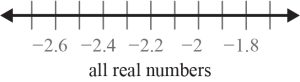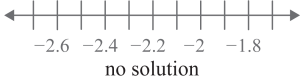Targeted Review Solutions

$(x + \sqrt{5}) (2 x - \sqrt{3}) + \sqrt{15}$

$2 x^{2} - x \sqrt{3} + 2 x \sqrt{5} - \sqrt{15} + \sqrt{15}$

$2 x^{2} - x \sqrt{3} + 2 x \sqrt{5}$

$(i^{36}) (i^{17})$

${(i^{4})}^{9} {(i^{4})}^{4} (i) {(1)}^{9} {(1)}^{4} (i)$

$(2 + 3 i) (7 - i^{3})$

$14 - 2 i^{3} + 21 i - 3 i^{4} 14 - 2 (- i) + 21 i - 3 (1) 14 + 2 i + 21 i - 3$

$11 + 23 i$

$\frac{y}{3 + \sqrt{x}}$

$\frac{y}{3 + \sqrt{x}} (\frac{3 - \sqrt{x}}{3 - \sqrt{x}})$

$\frac{3 y - y \sqrt{x}}{9 - x}$

Describe the end behavior for the function: $m (x) = \sqrt{x - 8} - 2$

$a = 1, h = 8, k = - 2$

$As x \to \infty, m (x) \to \infty, and as x \to 8, m (x) \to - 2$

Solve. Graph solutions on a number line.

$\sqrt{x + 5} \geq \sqrt{3 - x}$

$\begin{array}{rcl} \begin{matrix} Restrictions & Solve \\ x + 5 \geq 0 x \geq - 5 & 3 - x \geq 0 x \leq 3 & {(\sqrt{x + 5})}^{2} \geq {(\sqrt{3 - x})}^{2} x + 5 \geq 3 - x 2 x \geq - 2 x \geq - 1 \end{matrix} \end{array}$

$x > \sqrt{2 x + 3}$

$\begin{array}{rcl} \begin{matrix} Restrictions & Solve \\ 2 x + 3 \geq 0 & {(x)}^{2} > {(\sqrt{2 x + 3})}^{2} \\ 2 x \geq - 3 & x^{2} > 2 x + 3 \\ x \geq - 1.5 & x^{2} - 2 x - 3 > 0 \\ (x - 3) (x + 1) > 0 \\ x > 3 x > - 1 \end{matrix} \end{array}$

Name the domain and range of the absolute value parent function in set builder notation.

$\begin{array}{rcl} domain : \{x | x \in ℝ\}, range : \{y | y \in ℝ, y \geq 0\} \end{array}$

Multiple Choice

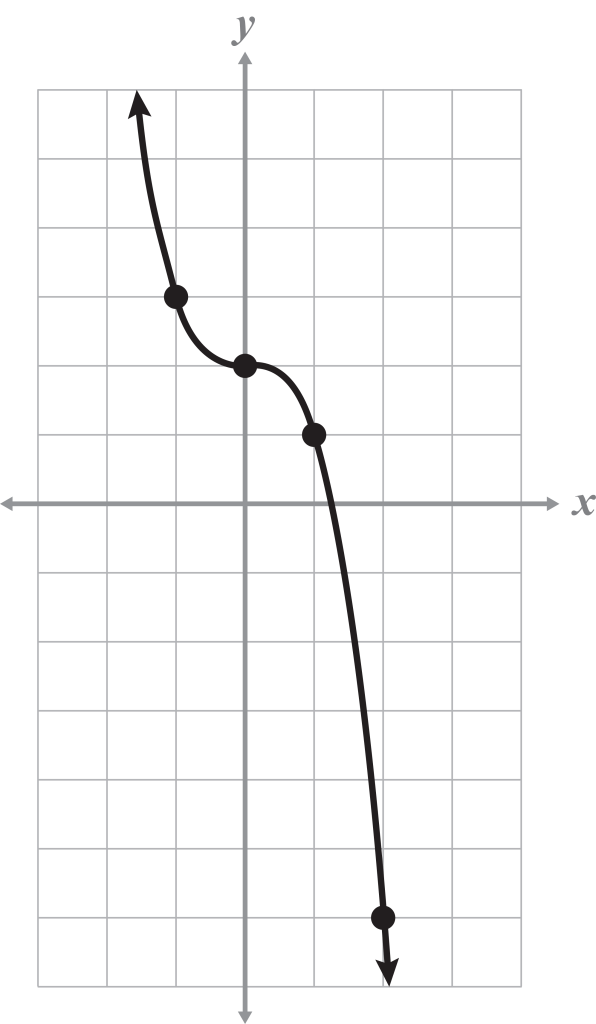
Which type of equation would best represent the given graph?

absolute value
cubic
square root
quadratic

no work is needed for this problem

Note

A, C, D) These equations do not represent the shape of the given graph.

Choose the best description of the transformation of the quadratic parent function for the equation:
$q (x) = 2 {(x + 8)}^{2} - 11$

The graph is vertically stretched by a factor of 2, moved 8 spaces left, and 11 spaces down from the parent graph.
The graph is vertically compressed by a factor of 2, moved 8 spaces right, and 11 spaces down from the parent graph.
The graph is vertically compressed by a factor of 2, moved 8 spaces left, and 11 spaces down from the parent graph.
The graph is vertically stretched by a factor of 2, moved 8 spaces right, and 11 spaces down from the parent graph.

no work needed for this problem

Note

A, D) The graph is compressed because $a = 2$

B, D) The graph moves left 8 spaces because $h = - 8$

Find the perimeter of a rectangle with a length of $6 x + 7$ units and a width of $4 x - 1$ units.

10x + 6 units
20x + 12 units
$24 x^{2} + 22 x - 7$ square units
20x + 12 square units

$P = 2 (l + w) P = 2 (6 x + 7 + 4 x - 1) P = 2 (10 x - 6) P = 20 x + 12$

Note

This option is the sum before multiplying by two.
This option is the area of the rectangle and perimeter is not in square units.
This option is not possible because the perimeter is not in square units.

Solve: $- |5 x + 11| > 1$

Note

This option is the solution if the negative sign in the given inequality is ignored.
This option is the solution if both cases of the inequality are solved. However, none of the values will make the inequality true.
This option is not possible, no value makes this true.

$|5 x + 11| < - 1$

No solution, absolute value cannot be less than a negative number.

Problem	1	2	3	4	5	6	7	8	9	10	11	12
Origin	L12	L15	L16	L12	L18	L14	L14	L17	L17	L18	A1	A1

L = Lesson in this level, A1 = Algebra 1: Principles of Secondary Mathematics, FD = Foundational Knowledge