Practice 2 Solutions

1. Explain how you can check to determine if the equation you found is the inverse.

Sample: To check if the inverse is correct, start with$f\left(a\right)=b$ and then substitute b into the new equation. If the result is a, then the inverse is correct.

2. $R=\left\{\left(–3, 12\right), \left(–6, 7\right), \left(1, 3\right), \left(–12, 12\right)\right\}$

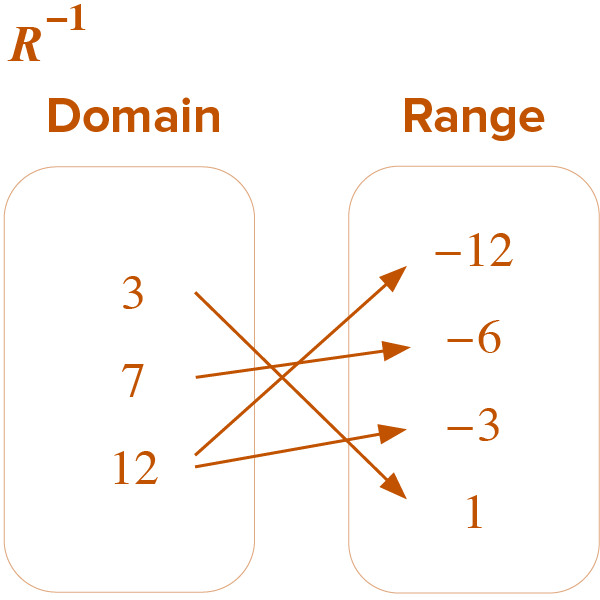
The relation is a function, but the inverse is not a function.

3. $R=\left\{\left(3, 4\right), \left(9, 2\right), \left(–6, 1\right), \left(4, 3\right), \left(2, –1\right)\right\}$

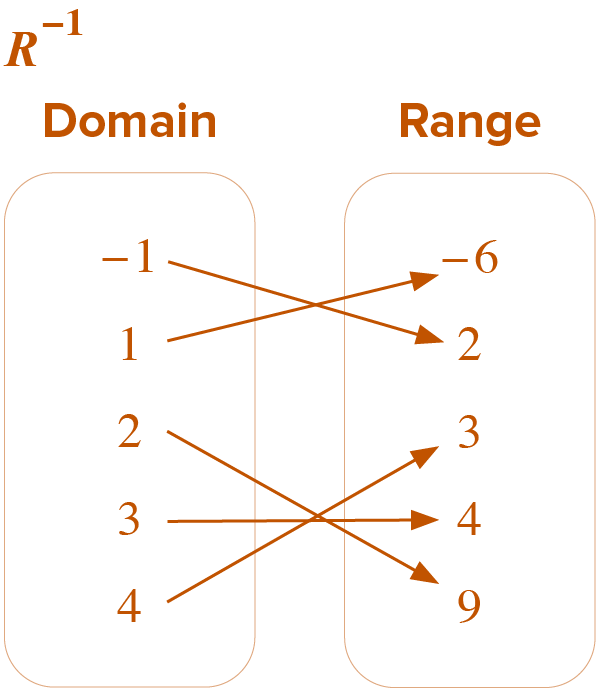
The relation and inverse are both functions.

4. The same class from Practice 1 was asked to list their favorite sport. The results were: R = {(Maddie, softball), (Hope, volleyball), (Stetson, soccer), (Austin, baseball), (Natalee, volleyball)}.

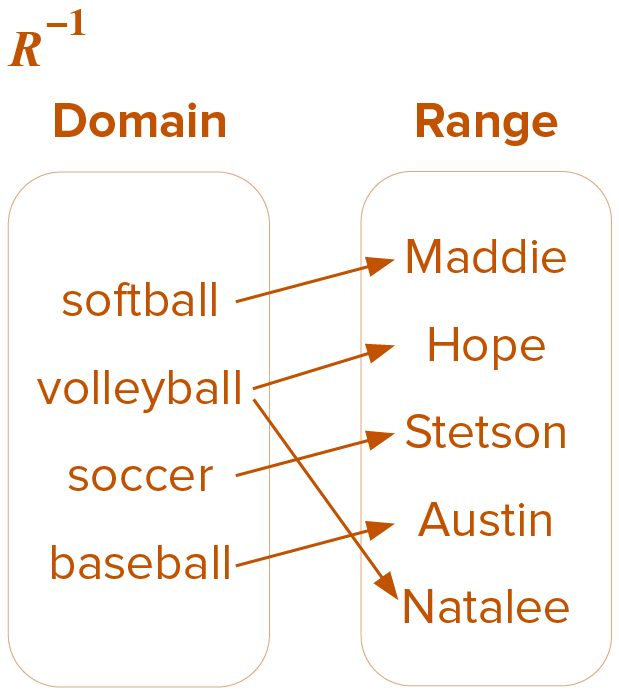
The relation is a function, but the inverse is not a function.

5. $f\left(x\right)=–{\left(x–2\right)}^3+2 g\left(x\right)=\sqrt[3]{–x+2}+2$

$\begin{array}{ccc}f\left(3\right)=–{(3–2)}^3+2& & g\left(1\right)=\sqrt[3]{–1+2}+2\\ f\left(3\right)=1& & g\left(1\right)=3\end{array}$

$f\left(x\right)$ and $g\left(x\right)$ are inverses.

6. $f\left(x\right)=x^2+3 g\left(x\right)=\sqrt{x+3}$

$$\begin{gathered} \begin{array}{ccc}f\left(3\right)=3^2+3 \\ f\left(3\right)=12& & g\left(12\right)=\sqrt{12+3} \\ g\left(12\right)=\sqrt{15}\end{array} \end{gathered}$$

$f\left(x\right)$ and $g\left(x\right)$ are not inverses.

7. $f\left(x\right)=2x+5 g\left(x\right)=\frac{x–5}{2}$

$$\begin{gathered} \begin{array}{ccc}f\left(3\right)=2\left(3\right)+5 \\ f\left(3\right)=11& & g\left(11\right)=\frac{11–5}{2} \\ g\left(11\right)=3\end{array} \end{gathered}$$

$f\left(x\right)$ and $g\left(x\right)$ are inverses.

8. $f\left(x\right)=\frac{2}{3}x+1$, check with $x=6.$

$$\begin{gathered} \begin{array}{rcl}& & \begin{array}{ccc}x=\frac{2}{3}y+1 \\ x–1=\frac{3}{2}y \\ y=\frac{3}{2}\left(x–1\right)& & f\left(6\right)=\frac{2}{3}\left(6\right)+1 \\ f\left(6\right)=5\\ & & f^{–1}\left(5\right)=\frac{3}{2}\left(5–1\right) \\ {f}^{–1}\left(5\right)=6\end{array}\end{array} \end{gathered}$$

$\begin{array}{rcl} f^{–1}\left(x\right)& =& \frac{3}{2}\left(x–1\right)\end{array}$

9. $f\left(x\right)=\sqrt{x+4}$ for $x\ge – 4,$ check with $x=5.$

$$\begin{gathered} \begin{array}{rcl}& & \begin{array}{ccc}x=\sqrt{y+4} \\ {x}^2=y+4 \\ {x}^2–4=y \\ y=x^2–4& & f\left(5\right)=5\sqrt{5+4} \\ f\left(5\right)=3\\ & & f^{–1}\left(3\right)={\left(3\right)}^2–4 \\ {f}^{–1}\left(3\right)=5\end{array}\end{array} \end{gathered}$$

$\begin{array}{rcl} f^{–1}\left(x\right)& =& x^2–4\end{array}$

10. $h\left(x\right)=\frac{1}{x+2}–3, x\ne –2$, check with $x=2.$

$$\begin{gathered} \begin{array}{rcl}& & \begin{array}{ccc}x=\frac{1}{y+2}–3 \\ x+3=\frac{1}{y+2} \\ \left(x+3\right)\left(y+2\right)=1 \\ y+2=\frac{1}{x+3} \\ y=\frac{1}{x+3}–2& & h\left(2\right)=\frac{1}{2+2}–3 \\ h\left(2\right)=–2.75\\ & & h^{–1}\left(–2.75\right)=\frac{1}{–2.75+3}–2 \\ {h}^{–1}\left(–2.75\right)=\frac{1}{0.25}–2=4–2 \\ {h}^{–1}\left(–2.75\right)=2\end{array}\end{array} \end{gathered}$$

$\begin{array}{rcl}{h}^{–1}\left(x\right)& =& \frac{1}{x+3}–2\end{array}$

11. $f\left(x\right)=\frac{2}{5}x+7$, check with $x=5.$

$$\begin{gathered} \begin{array}{rcl}& & \begin{array}{ccc}x=\frac{2}{5}y+7 \\ x–7=\frac{2}{5}y \\ \frac{5}{2}\left(x–7\right)=y& & f\left(5\right)=\frac{2}{5}\left(5\right)+7 \\ f\left(5\right)=9\\ & & f^{–1}\left(9\right)=\frac{5}{2}\left(9–7\right) \\ {f}^{–1}\left(9\right)=5\end{array}\end{array} \end{gathered}$$

$\begin{array}{rcl} f^{–1}\left(x\right)& =& \frac{5}{2}\left(x–7\right)\\ & & {\mathrm{Domain}}_f:\left\{x\in \mathrm{ℝ}\right\}, {\mathrm{Range}}_f: \left\{y\in \mathrm{ℝ}\right\}\\ & & {\mathrm{Domain}}_{f^{–1}}:\left\{x\in \mathrm{ℝ}\right\}, {\mathrm{Range}}_{f^{–1}}: \left\{y\in \mathrm{ℝ}\right\}\end{array}$

12. $g\left(x\right)=\frac{1}{4}{x}^2+3$, for $\left\{x|x\ge 0\right\}$ check with $x=3.$

$$\begin{gathered} \begin{array}{rcl}& & \begin{array}{ccc}x=\frac{1}{4}{y}^2+3 \\ x–3=\frac{1}{4}{y}^2 \\ 4\left(x–3\right)=y^2 \\ \pm 2\sqrt{x–3}=y& & g\left(3\right)=\pm 2\sqrt{3–3} \\ g\left(3\right)=\pm 2\sqrt{0} \\ g\left(3\right)=0\\ & & g^{–1}\left(0\right)=\frac{1}{4}{\left(0\right)}^2+3 \\ {g}^{–1}\left(0\right)=3\end{array}\end{array} \end{gathered}$$

$\begin{array}{rcl}{g}^{–1}\left(x\right)& =& 2\sqrt{x–3}\\ & & {\mathrm{Domain}}_f:\left\{x\in \mathrm{ℝ}, x\ge 0\right\}, {\mathrm{Range}}_f: \left\{y\in \mathrm{ℝ}, y\ge 3\right\}\\ & & {\mathrm{Domain}}_{f^{–1}}:\left\{x\in \mathrm{ℝ}, x\ge 3\right\}, {\mathrm{Range}}_{f^{–1}}: \left\{y\in \mathrm{ℝ}, y\ge 0\right\}\end{array}$