Mastery Check Solution

Show What You Know

Find a solution to the problem. Show your work.

Use the number set: {1, 2, 3, 4, 5, 6}
Use each number only once.
The product of the binomials must be a real number.

$(1 + 2 i) (3 - 6 i) 3 - 6 i + 6 i - 12 i^{2} 3 + 12 15$

$(1 + 3 i) (2 - 6 i) 2 - 6 i + 6 i - 18 i^{2} 2 + 18 20$

$(6 + 2 i) (3 - 1 i) 18 - 6 i + 6 i - 2 i^{2} 18 + 2 20$

$(6 + 3 i) (2 - 1 i) 12 - 6 i + 6 i - 3 i^{2} 12 + 3 15$

$(2 + 4 i) (3 - 6 i) 6 - 12 i + 12 i - 24 i^{2} 6 + 24 30$

$(2 + 3 i) (4 - 6 i) 8 - 12 i + 12 i - 18 i^{2} 8 + 18 26$

$(6 + 4 i) (3 - 2 i) 18 - 12 i + 12 i - 8 i^{2} 18 + 8 26$

$(6 + 3 i) (4 - 2 i) 24 - 12 i + 12 i - 6 i^{2} 24 + 6 30$

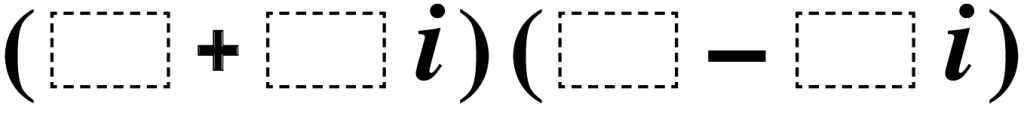
Note

There are 8 possible solutions to this problem given the set of numbers. You only need to find one, but you may be able to identify other solutions once you find the numbers that will cause the middle two terms to simplify out using the distributive property.

Cross values out rather than erasing them so you can keep track of the values you have already used.

Q: What must simplify out of the problem so that the result is a real number?

A: Any terms with the imaginary unit i.

Q: What is the definition of the imaginary unit?

A: $i^{2} = - 1$

Q: Why might knowing the definition of i be helpful for this problem?

A: Because one of the terms will have $i^{2}$ which will simplify to –1.

Q: Why are the binomials that you created not conjugates?

A: Because conjugates have to have the same terms in both expressions, only with different signs. All of the terms are different in the expressions since you cannot repeat any numbers.

Say What You Know

In your own words, talk about what you have learned using the objectives for this part of the lesson and your work on this page.

Note

Restate the objectives of the lesson in your own words. If you are unable to restate the lesson objectives, go back and reread the objectives and then explain them.

- Simplify expressions with complex numbers in the form of a + bi, where a and b are real numbers, using addition, subtraction, and multiplication.
- Solve identities with complex numbers.
- Rationalize the denominator with complex conjugates.