Explore

Transformations of Parent Functions Solutions

Note

Transformations of linear and quadratic functions are covered in Algebra 1. These transformations will be in the practice problems, but will not be in the examples. Transformations of reciprocal functions were covered in the previous unit.

You can describe the transformation of an equation or graph by comparing it to its parent function using a, h, and k.
The values a, h, and k reveal the transformation of the function in general form .
The general form of a function can be thought of as a formula for that type of function.
Once you identify the type of function , you can describe the transformation.

Function Name

General Form of the Function

Linear

$f (x) = a (x - h) + k$

Note

This is point-slope form with $k = y_{1}$ added to the right side of the equation.

Absolute Value

Quadratic

Square root

$\begin{matrix} f (x) = a |x - h| + k \\ f (x) = a {(x - h)}^{2} + k \\ f (x) = a \sqrt{x - h} + k \end{matrix}\}$

For these functions, the ordered pair $(h, k)$ is used to determine the parts of the domain, range, and end behavior

Cubic

$f (x) = a {(x - h)}^{3} + k$

Cube root

$f (x) = a \sqrt[3]{x - h} + k$

Rational

$f (x) = \frac{a}{x - h} + k, x \neq h$

The value a will reflect and/or dilate the graph.
- – a reflects the graph across/over the x-axis.

Note

In addition to “across” and “over,” be aware that the word “about” is also commonly used to describe reflection.

- $| a | > 1$ stretches the graph vertically.
- $0 < | a | < 1$ compresses the graph vertically.
The value h will translate or shift the graph horizontally .
- (x – h) moves the graph right → .
- (x + h) moves the graph left ← .
The value k will translate or shift the graph vertically .
- + k moves the graph up ↑.
- – k moves the graph down ↓.
f (–x) reflects the graph across/over the y-axis.

Note

This lesson will only reflect the square root function over the y-axis.

Vertex form for functions can be used to describe transformations.

Note

Remember to use your notes and Formula Sheet to remind yourself what the parent graphs look like on the coordinate plane.

See the More to Explore activity to learn about using technology to transform graphs.

Example 1

Name the type of function. Then write the equation and explain the given transformation.

Plan

Name the type of function

Mark key points on given graph

Sketch the parent graph

Identify a, h, k

Write the equation

Implement

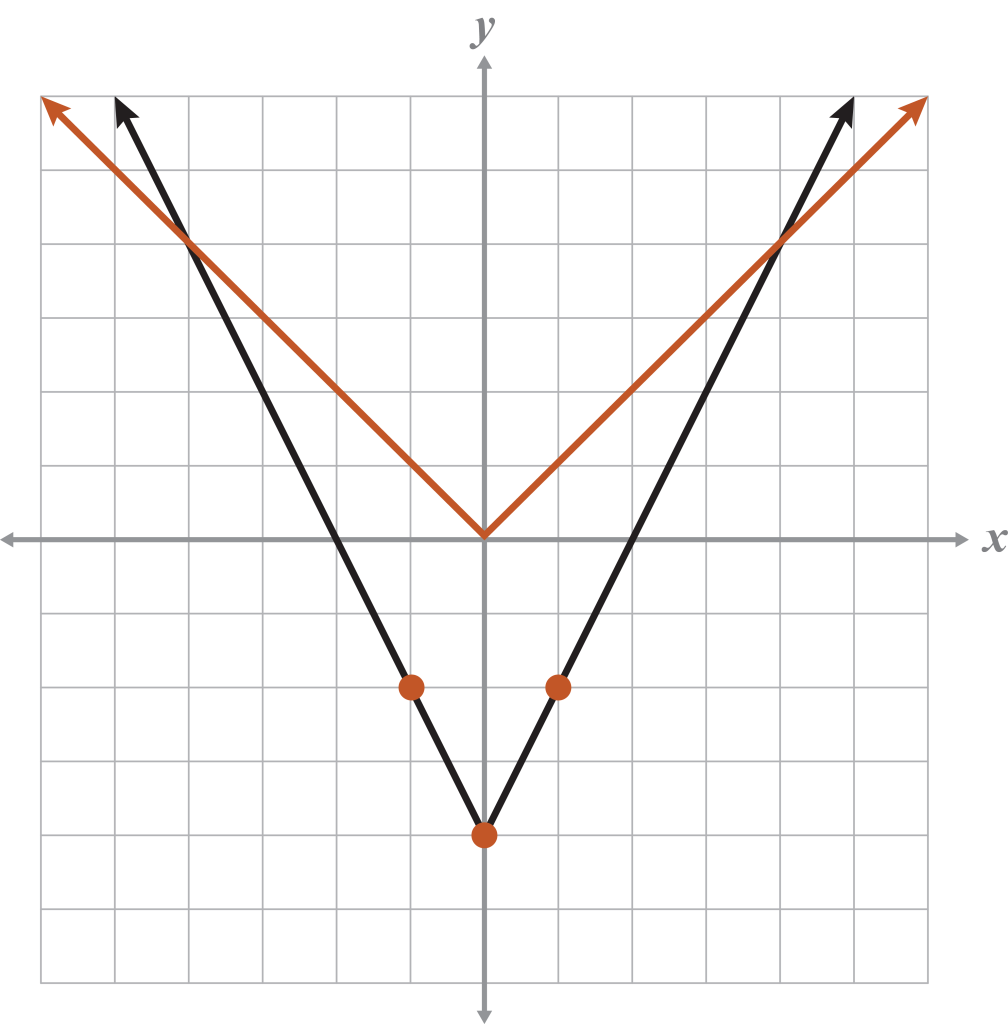
Type of function: Absolute value, $y = a |x - h| + k$

Identify a, h, k: $a = 2, h = 0, k = - 4$

Equation: $y = 2 |x| - 4$

Explain

The graph stretches vertically by a factor of 2 and translates down 4 spaces as compared to the absolute value parent function. This occurs because $a = 2$ , and $k = - 4 .$

Note

Sketching the parent function is optional but provides a good frame of reference for transformations and determining the values of a, h, and k.

Example 2

Name the type of function. Then write the equation and explain the given transformation.

$Cubic, y = a {(x - h)}^{3} + k a = - 1, h = - 2, k = 1 y = - {(x + 2)}^{3} + 1$

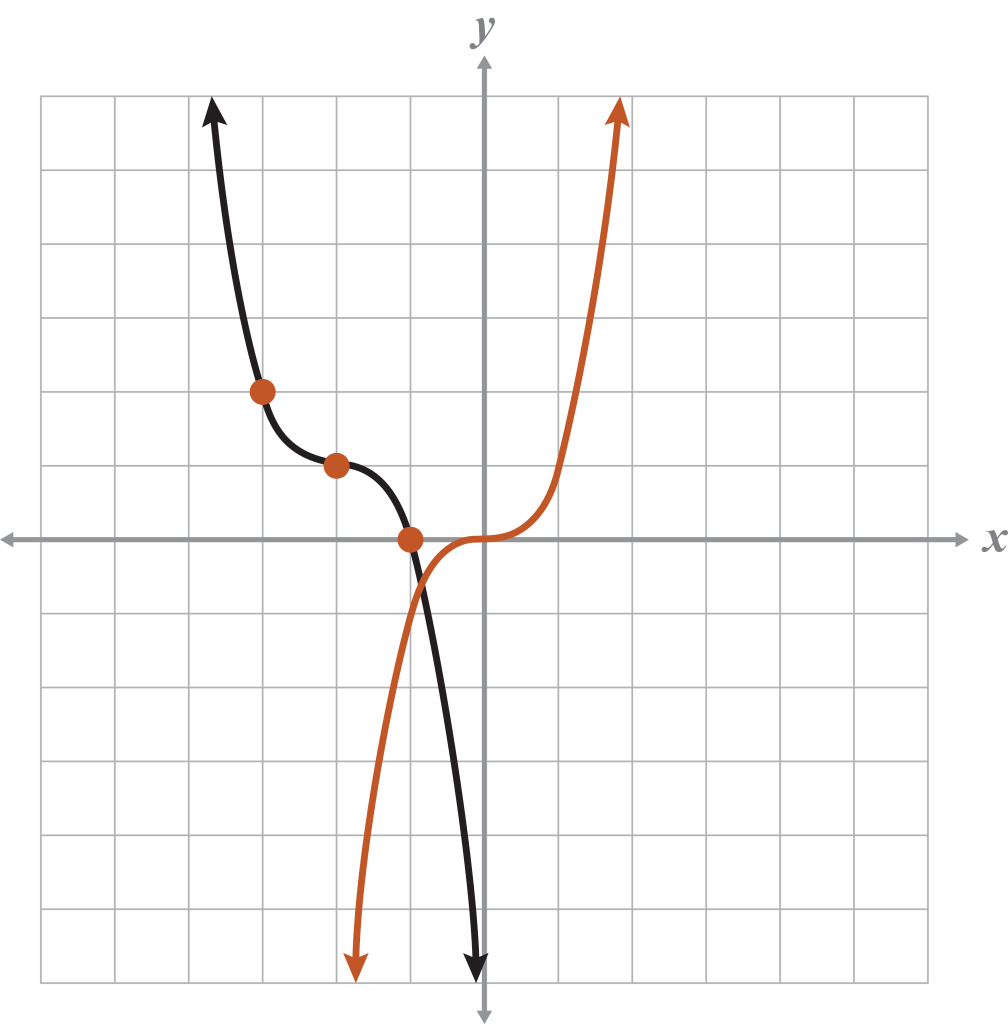
The cubic graph is a reflection with a horizontal translation left 2 spaces and a vertical translation up one space.

Note

Sketching the parent function is helpful because it is used to compare the transformed function to the parent graph. In this case, the end behavior changes for the y-values, which means that $a = - 1$ .

Example 3

Use the equation to name the type of function and describe the transformations occurring to the parent function.

$f (x) = \frac{1}{4} \sqrt{(12 - x)} + 7$

$a = \frac{1}{4}, h = 12, k = 7$

$f (- x)$ : reflect over the y-axis

The square root function would reflect over the y-axis because $12 - x$ .

The graph would be compressed vertically by a factor of $\frac{1}{4}$ because $a = \frac{1}{4} .$

The function would also shift right 12 units and shift up 7 units because $h = 12 and k = 7 .$