Explore

End Behavior of Functions Solutions

End behavior is an important feature of a graph because it shows trends.
The end behavior of a graph is a trend in the f (x) values when x approaches positive infinity (+∞) and when x approaches negative infinity (–∞) .
Another way to think about end behavior is to ask yourself:
- As x gets bigger, what happens to y ?
  AND
- As x gets smaller, what happens to y ?
The notation for end behavior is written as:

As $x \to + \infty, f (x) \to$ , and as $x \to - \infty, f (x) \to$

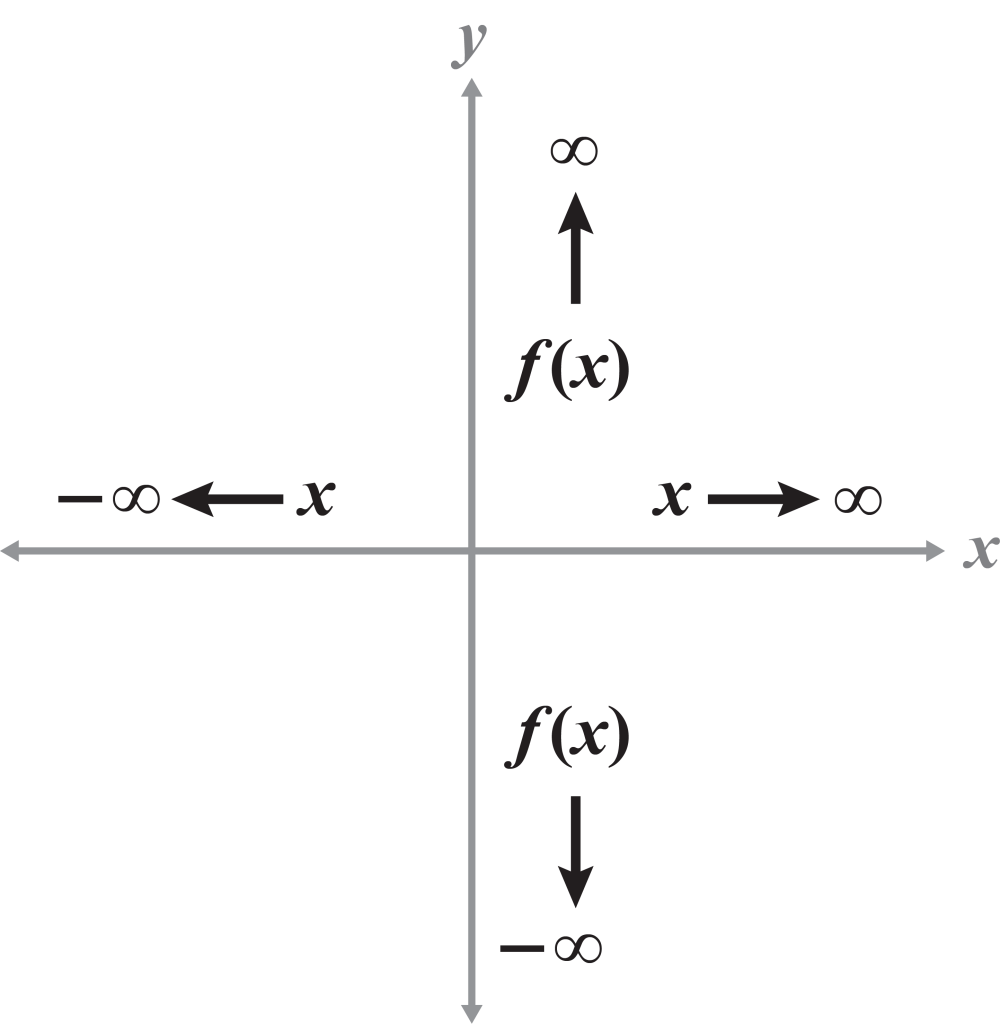
The notation for end behavior is said as:

“As x approaches positive infinity, the function approaches [blank], and as x approaches negative infinity, the function approaches [blank].”

The blanks are determined by what the graph looks like.
The arrows on the end(s) of a graph on the coordinate plane demonstrate the direction of the end behavior of a graph.
When a function is written in standard form, use the leading coefficient and the degree of the function (rather than the graph) to determine the end behavior.
Recall that degree is the value of the largest exponent.

Note

This concept will be discussed in more detail in later lessons.

You did this in Algebra 1 when you looked at the meaning of rate of change in problems.

It is possible that a graph will start or end with a point. When this happens, the notation of the end behavior will use the point rather than the infinity symbols.

Example 1

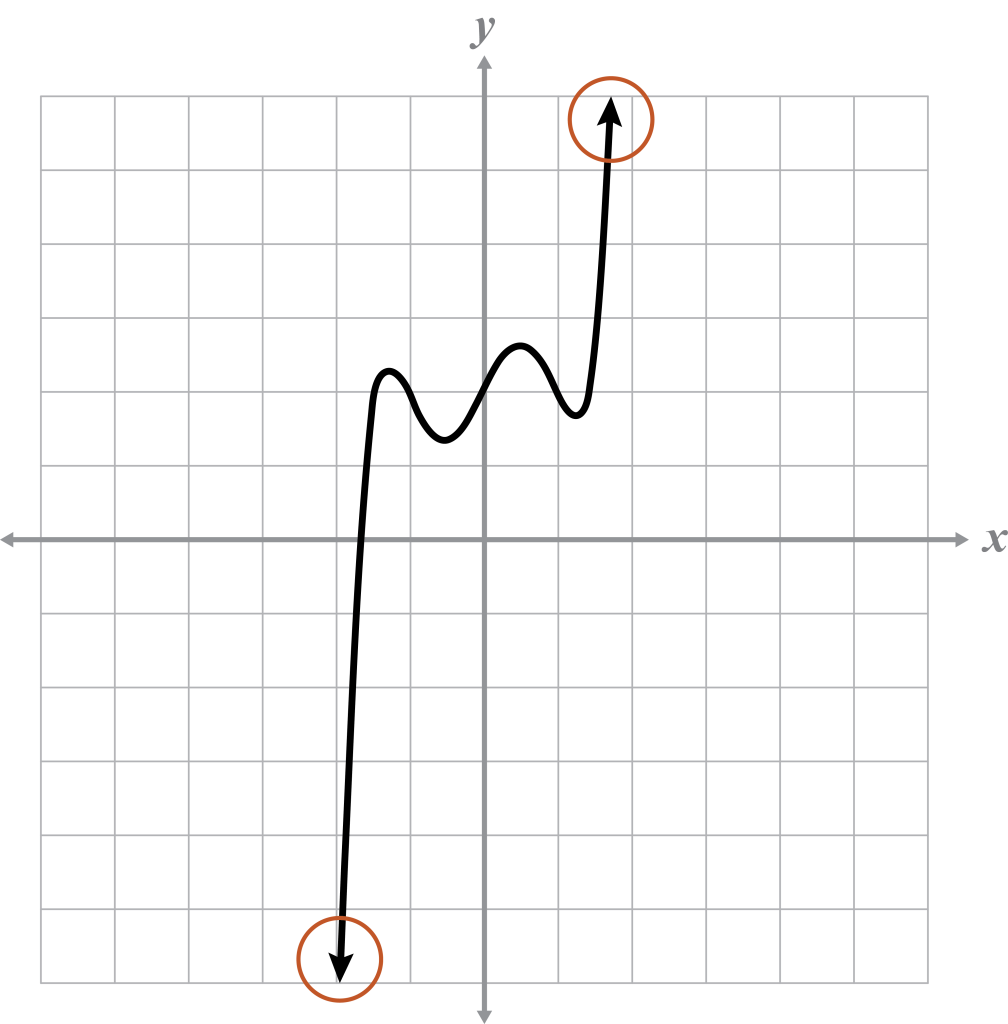
Name the end behavior of the odd degree graph.

Plan

Find and circle the ends of the graph.

As x increases and decreases, determine what happens to the y-values.

Implement

Explain

Written notation:

As $x \to + \infty, f (x) \to + \infty,$ and as $x \to - \infty, f (x) \to - \infty$

Spoken word:

As x approaches positive infinity, the y (or f (x)) approaches positive infinity.

And, as x approaches negative infinity, the y (or f (x)) approaches negative infinity.

Note

This graph is an odd degree function because the ends are pointing in opposite directions.

Example 2

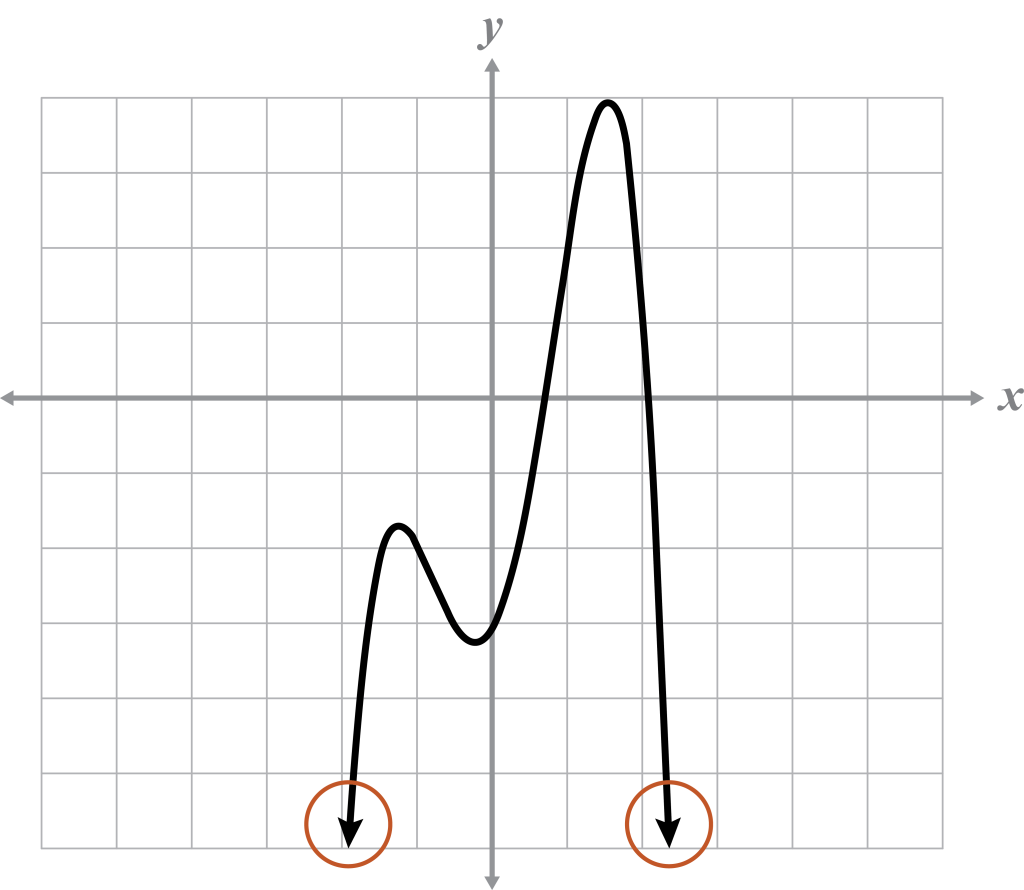
Name the end behavior of the even degree graph.

As $x \to + \infty, f (x) \to - \infty$ and as $x \to - \infty, f (x) \to - \infty$

Note

This graph is an even degree function because both ends point in the same direction.