The Horizontal Line Test Solutions

• The    horizontal line test (HLT)    is a visual representation that determines if the     inverse    of a graph on the coordinate plane is a function by running a horizontal line ↔ across the graph.

• If the horizontal line touches    more than one point     at a time, the inverse of the graph is not a function.

• The HLT also determines if a function is    one-to-one   .

• A one-to-one function has    one output    for each input. (In other words, the domain AND range values are both unique for a one-to-one function.)

Note

A graph can still be made on a coordinate plane even when a function does not exist.

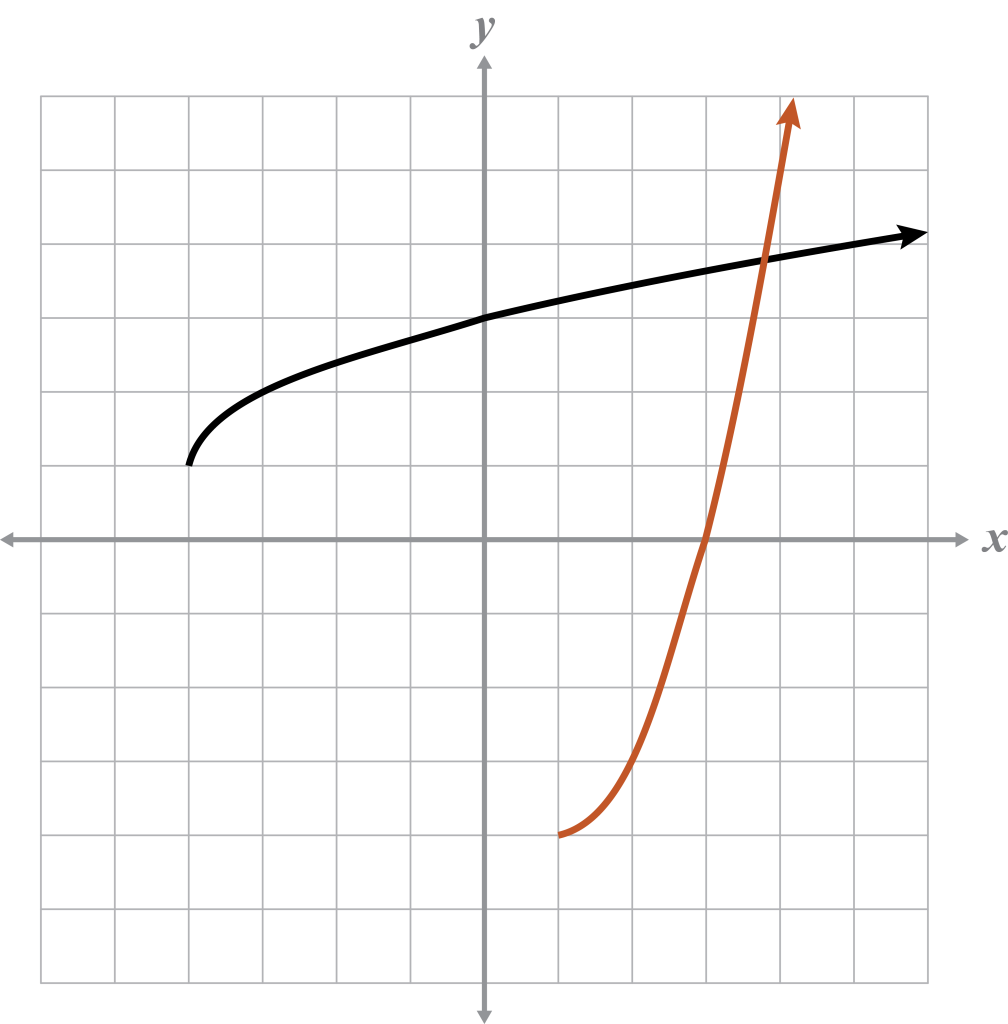
Example 4

For the given graph:

• • Name the domain and range for the graph and its inverse.
  • Explain whether or not the graph represents a function.
  • If the graph is a function, determine if it is one-to-one.
  • If the graph is a function, determine if the inverse is also a function.

Note

You can plot the inverse on the coordinate plane to help see if the inverse is a function using the VLT and determine the domain and range for the inverse if needed.

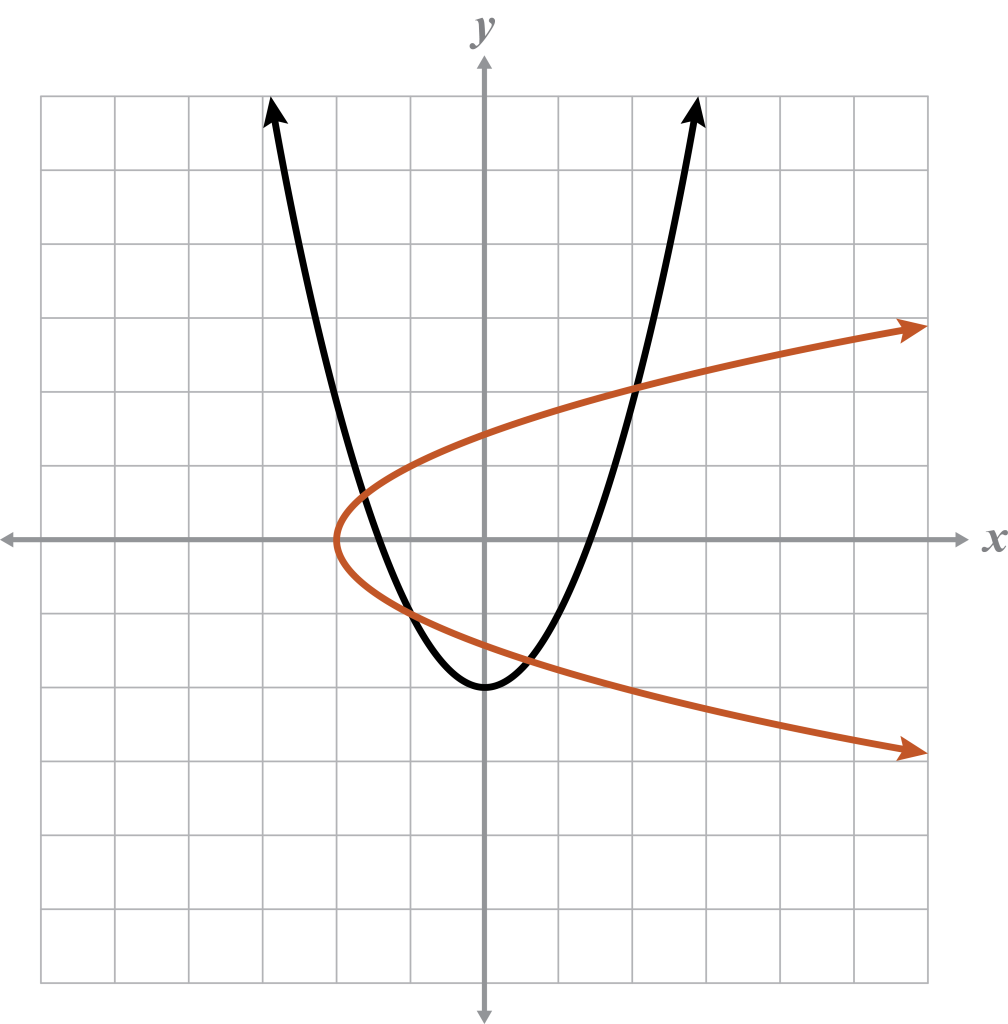
Example 5

For the given graph:


• • Name the domain and range for the graph and its inverse.

  • Explain whether or not the graph represents a function.

  • If the graph is a function, determine if it is one-to-one.

  • If the graph is a function, determine if the inverse is also a function.

Note

Naming the graph is good practice to retain recognition of equations graphically.

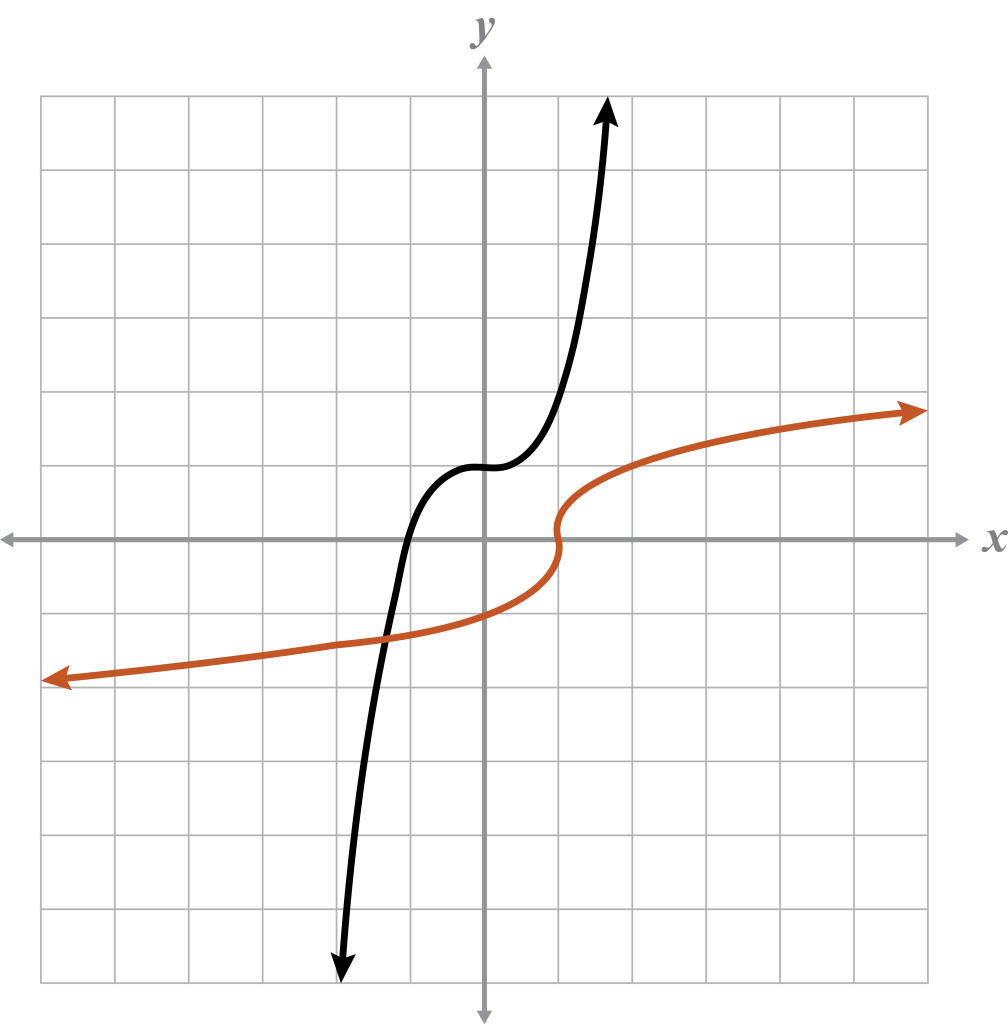
Example 6

For the given graph:

• • Name the domain and range for the graph and its inverse.

  • Explain whether or not the graph represents a function.

  • If the graph is a function, determine if it is one-to-one.

  • If the graph is a function, determine if the inverse is also a function.