Explore

Graphing Functions and Their Inverses Solutions

• When the graph of a function is given, graph the inverse function by    interchanging the domain and range values    and plotting them on the coordinate plane. 

• If the given function is defined as $f \left(a\right)=b$ and graphed as (a, b), then the inverse function can be defined as $\underline{ \mathbf{ }{\mathit{f}}^{\mathbf{–}\mathbf{1}}\mathbf{\left(}\mathit{b}\mathbf{\right)}\mathbf{=}\mathit{a} }$ and graphed as $\underline{ \mathbf{(}\mathit{b}\mathbf{,}\mathbf{ }\mathit{a}\mathbf{)} }$.

• When the inverse of a function is graphed it is    reflected    over the line y = x because the inverse of y = x is $\underline{\mathit{ }\mathit{ }\mathit{ }\mathit{x}\mathit{=}\mathit{y}\mathit{ }\mathit{ }\mathit{ }}$.

• The line of    reflection   , y = x, is used to confirm visually that the function and its inverse are correct on the coordinate plane. It is optional, and so can be drawn as a    dashed line   .

• Recall that the    Vertical Line Test (VLT)    is a visual representation that determines if a graph on the coordinate plane is a function by running a vertical line across the graph.

• If the vertical line touches    more than one point    at a time, the graph is not a function.

• The VLT can also be used to determine if the inverse of the given function is a    function   .

Example 1

Graph the inverse on the coordinate plane.

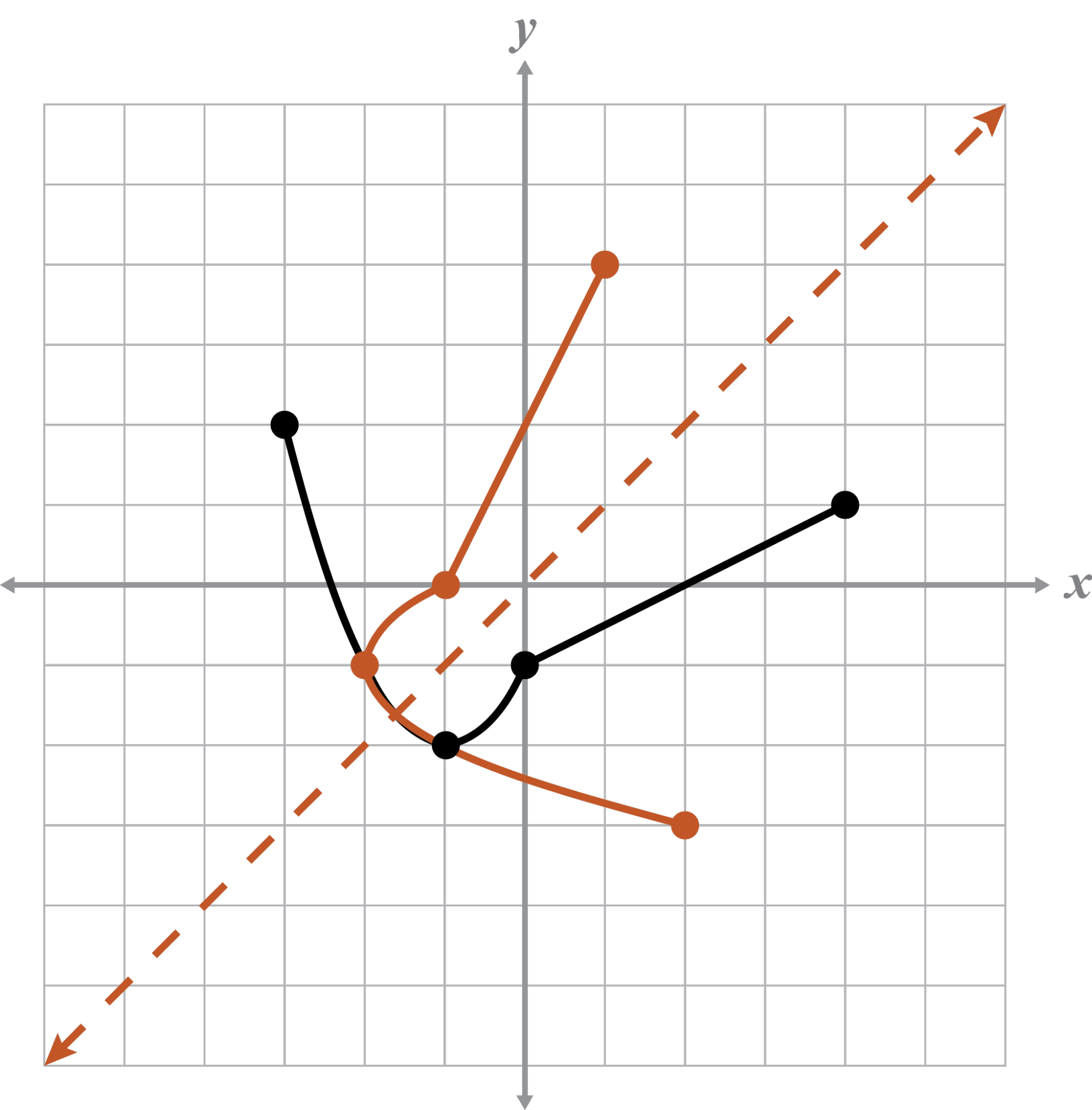
Example 2

Graph the inverse on the coordinate plane. Explain whether or not the graph and its inverse represent functions.

Example 3

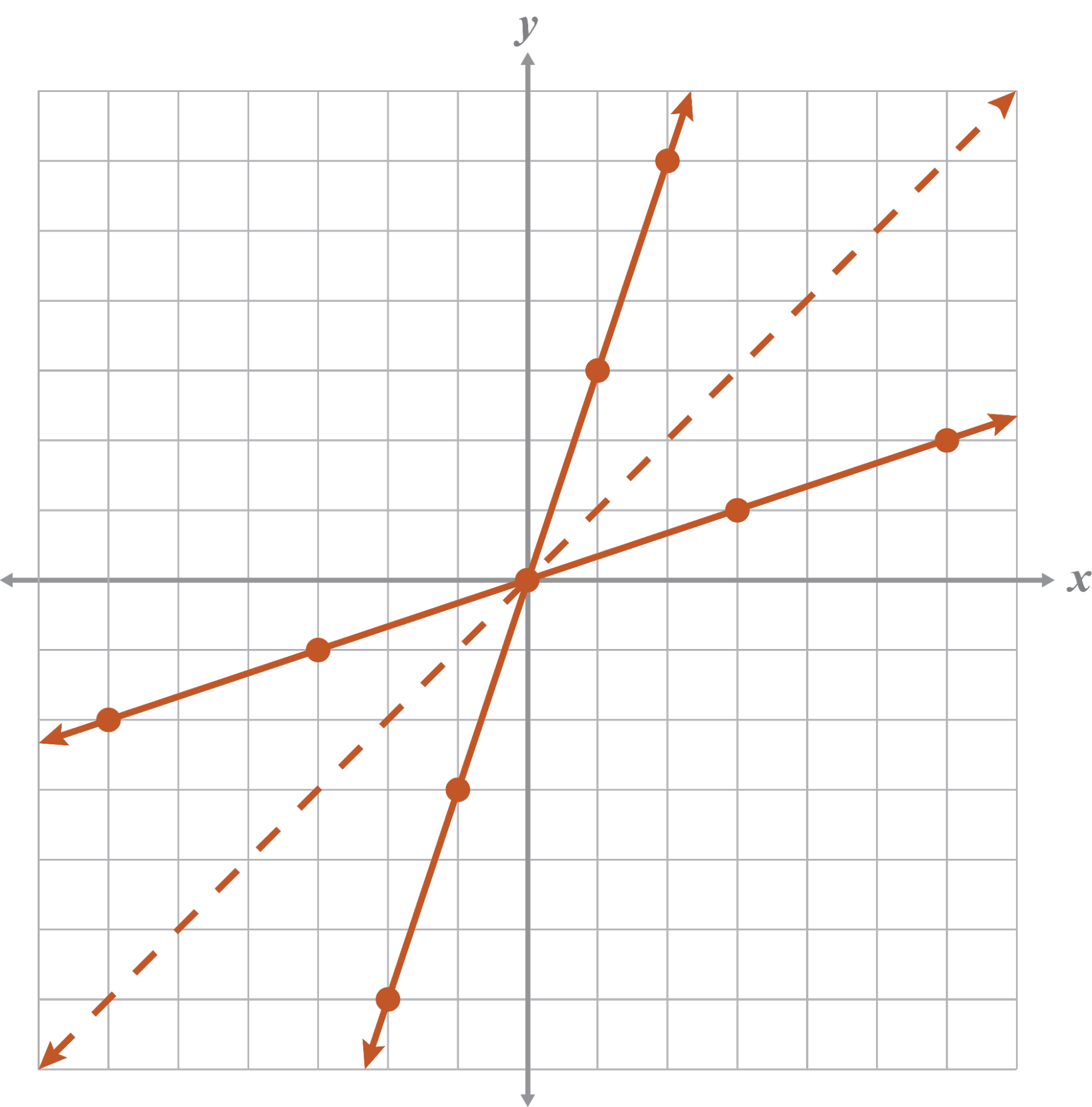
Find the inverse of the function algebraically. Then graph the function and its inverse on the coordinate plane. Explain whether or not the graph and its inverse represent functions.

Note

The function and its inverse intersect at the origin. Remember that the VLT should only be used to check one graph at a time.