Targeted Review Solutions

Simplify. Write answers in radical form.

$\sqrt[4]{162 x^{8} y^{14}}$

$\sqrt[4]{2 \cdot 3^{4} x^{8} y^{14}} 2^{\frac{1}{4}} \cdot 3^{\frac{4}{4}} x^{\frac{8}{4}} y^{\frac{14}{4}} 2^{\frac{1}{4}} \cdot 3^{1} x^{2} y^{3 \frac{2}{4}}$

$3 x^{2} |y^{3}| \sqrt[4]{2 y^{2}}$

$\frac{5 \sqrt{3}}{2} (\sqrt{\frac{3}{5}})$

$\frac{5 \sqrt{3}}{2} \cdot \frac{\sqrt{3}}{\sqrt{5}} = \frac{5 \sqrt{9}}{2 \sqrt{5}} \frac{5 (3)}{2 \sqrt{5}} = \frac{15}{2 \sqrt{5}} \frac{15}{2 \sqrt{5}} (\frac{\sqrt{5}}{\sqrt{5}}) \frac{15 \sqrt{5}}{2 (5)}$

$\frac{3 \sqrt{5}}{2}$

Simplify and name the numbers using all classifications for the set of real numbers.
${ℕ, 𝕎, ℤ, ℚ, 𝕀, ℝ}$

$\sqrt[3]{27} - 3$

3 – 3

0, $\{W, ℤ, ℚ, ℝ\}$

$\frac{1}{2^{- 1}}$

2, $\{ℕ, W, ℤ, ℚ, ℝ\}$

$\sqrt{12}$

$\sqrt{2^{2} \cdot 3}$

$2 \sqrt{3}, \{𝕀, ℝ\}$

$\frac{5 - 8}{8 - 2}$

$- \frac{3}{6}$

$- \frac{1}{2}, \{ℚ, ℝ\}$

Solve.

$\frac{x - 11}{x^{2} - 2} = \frac{6}{x}$

$\begin{array}{rcl} x & \neq & \pm \sqrt{2}, 0 \\ x (x - 11) & = & 6 (x^{2} - 2) \\ x^{2} - 11 x & = & 6 x^{2} - 12 \\ 5 x^{2} + 11 x - 12 & = & 0 \\ (x + 3) (5 x - 4) & = & 0 \end{array}$

$x = - 3, \frac{4}{5}$

Determine the value of Q to make the polynomial identity true.
${(3 x - Q)}^{2} = 9 x^{2} - 16 (3 x - 4)$

$\begin{array}{rcl} 9 x^{2} - 6 Q x + Q^{2} & = & 9 x^{2} - 48 x + 64 \\ - 6 Q x & = & - 48 x \\ - 6 Q & = & - 48 \end{array}$

Q = 8

Multiple Choice

Simplify.
$\frac{5}{\sqrt{6} - 4}$

$- \sqrt{3} + 2$
$\frac{- \sqrt{30} + 20}{10}$
$- \frac{\sqrt{6} + 4}{2}$
$\frac{\sqrt{6} + 4}{2}$

Note

This option incorrectly simplified out a 2. This is not possible because the coefficient of the radical is one.
This option multiplies a coefficient and a radicand together.
The negative sign is missing from the answer.

$\frac{5}{\sqrt{6} - 4} (\frac{\sqrt{6} + 4}{\sqrt{6} + 4}) \frac{5 \sqrt{6} + 20}{6 - 16} \frac{5 \sqrt{6} + 20}{- 10} \frac{5 (\sqrt{6} + 4)}{5 (- 2)} - \frac{\sqrt{6} + 4}{2}$

Determine the number line that best matches the solution to the compound inequality.
– 3x + 1 > 4 OR 3x + 1 ≥ 4

$\begin{matrix} - 3 x > 3 & OR & 3 x \geq 3 \\ x < - 1 & x \geq 1 \end{matrix}$

Note

There should be an open point at – 1 and a closed point at 1.
This option represents an AND inequality, not an OR inequality.
The points are marked, but the number line is not shaded.

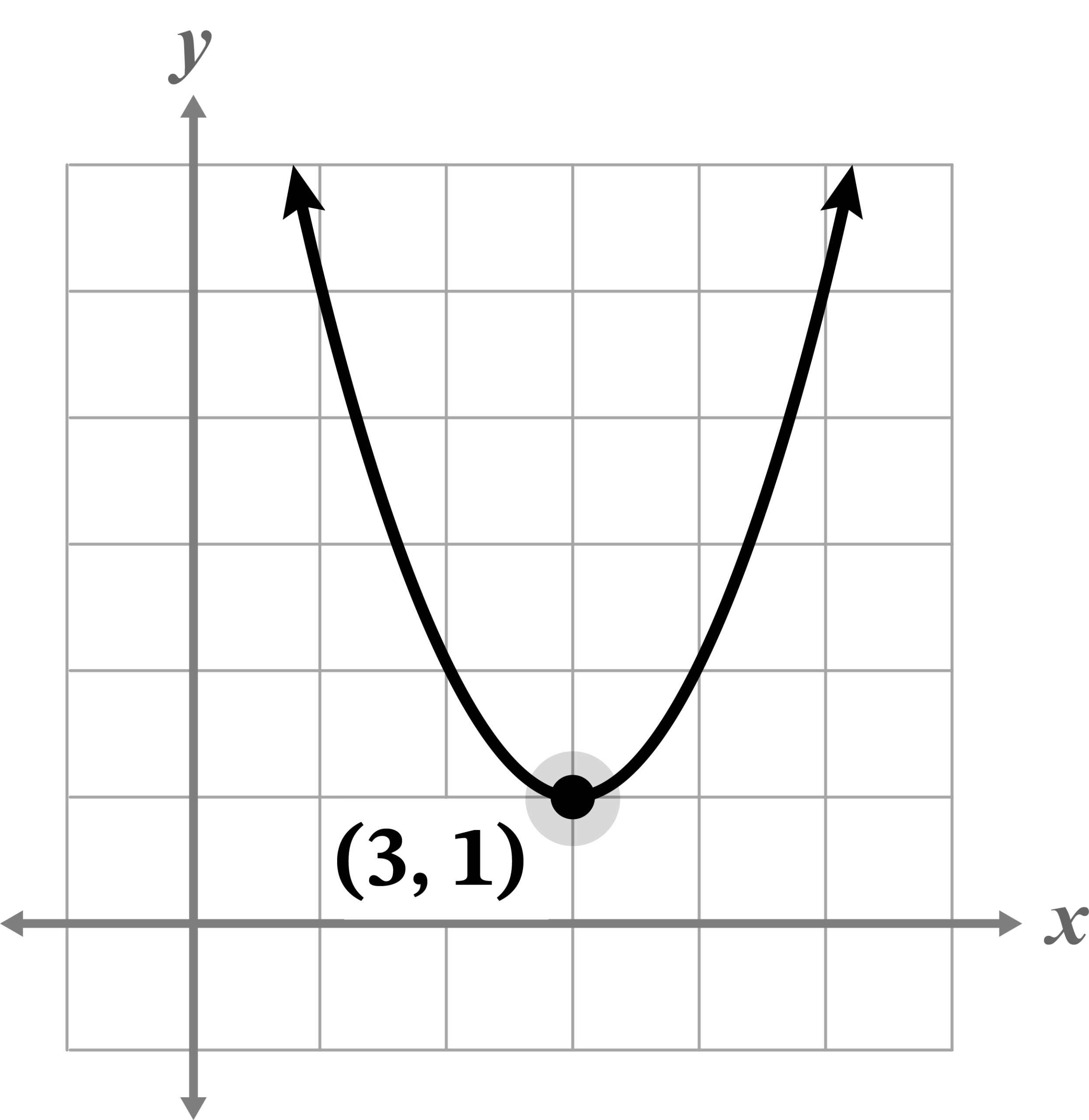
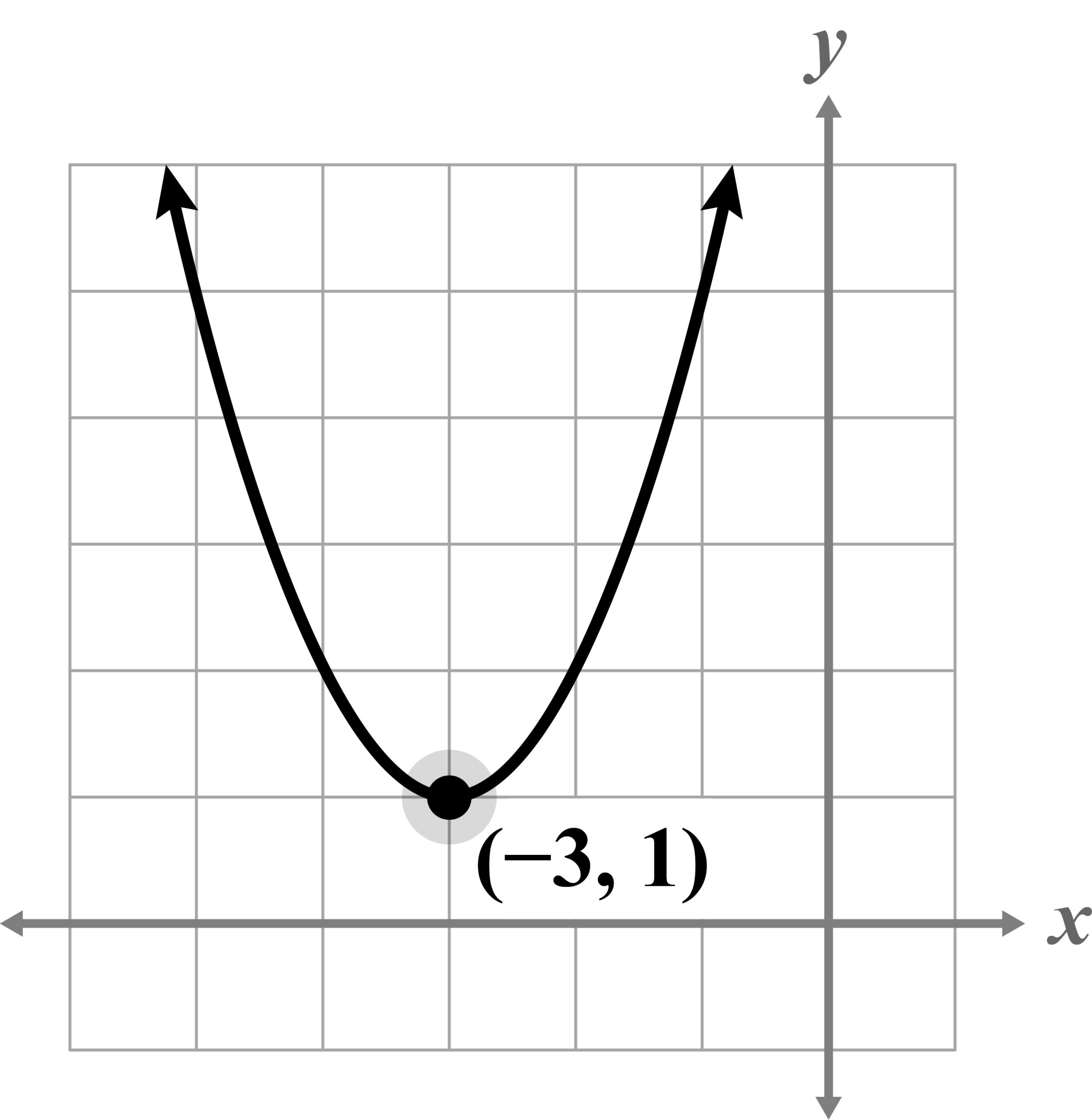
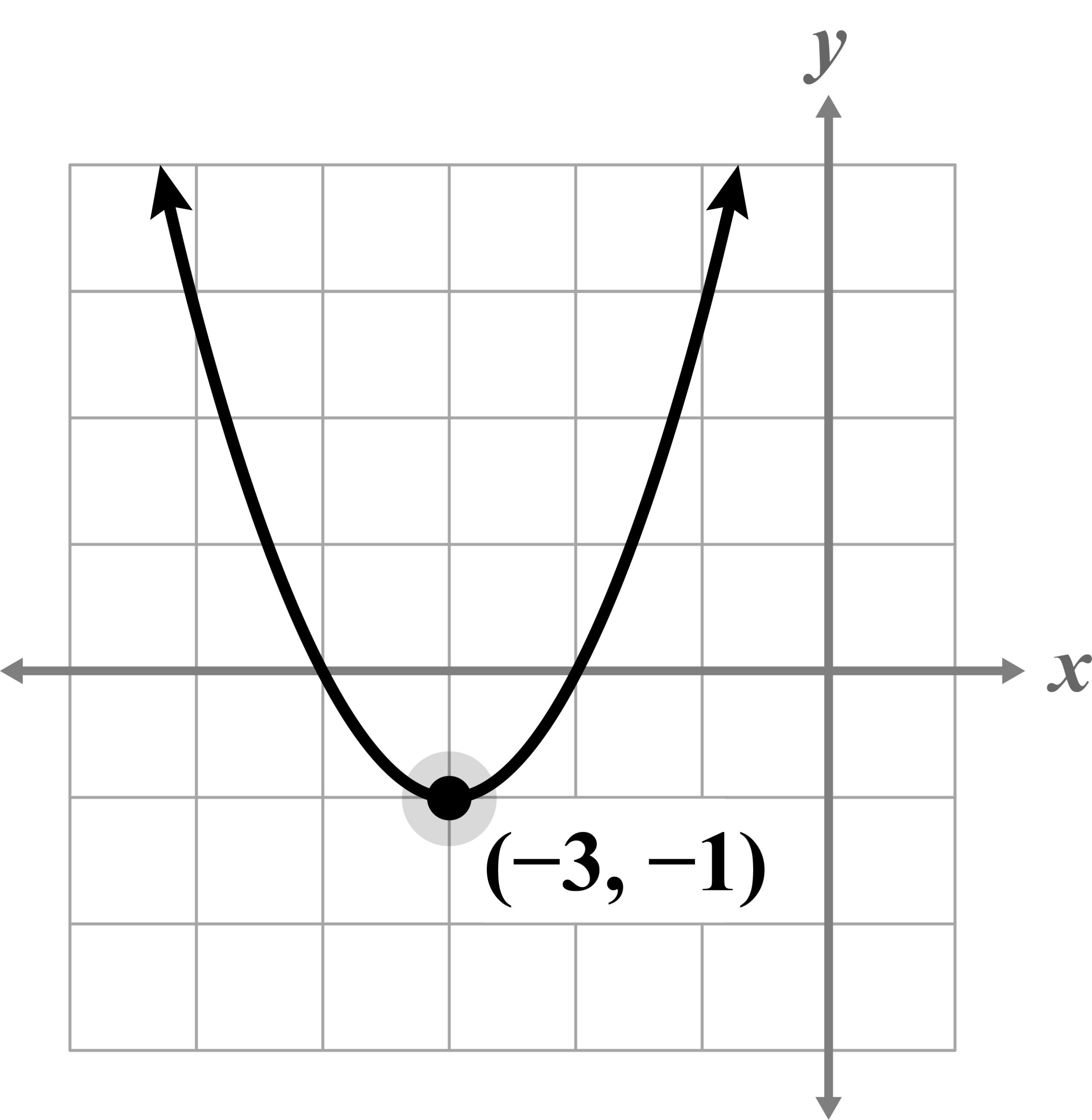
Select the graph of the quadratic function $g (x) = {(x - 3)}^{2} + 1.$

Vertex form of a parabola is $y = {(x - h)}^{2} + k$ .

(h, k) = (3, 1)

h shifts the graph right 3 spaces and k shifts the graph up 1 space

Note

B, C) These options have the opposite sign for h, making the graph shift left rather than right.

C, D) These options have the opposite sign for k, making the graph shift down rather than up.

Select the expressions that form conjugates.

$(3 \sqrt{2})$
$(3 \sqrt{2} + 1)$
$(3 \sqrt{2} - 1)$
± 1

Note

Conjugates are written in the form $(a \sqrt{b} - c \sqrt{d})$ and $(a \sqrt{b} + c \sqrt{d})$ where the terms are identical for both binomials, but one pair adds and the other pair subtracts the terms.

Problem	1	2	3	4	5	6	7	8	9	10	11	12
Origin	L11	L12	A1	A1	A1	A1	L9	L4	L12	A1	A1	L12

L = Lesson in this level, A1 = Algebra 1: Principles of Secondary Mathematics, FD = Foundational Knowledge