Practice 1 Solutions

Simplify. Rationalize the denominator. Assume all variables are positive.

$\frac{5}{3 \sqrt{8}}$

$\frac{5}{3 \cdot 2 \sqrt{2}} = \frac{5}{6 \sqrt{2}} \frac{5}{6 \sqrt{2}} (\frac{\sqrt{2}}{\sqrt{2}}) \frac{5 \sqrt{2}}{6 \sqrt{2^{2}}} \frac{5 \sqrt{2}}{6 \cdot 2}$

$\frac{5 \sqrt{2}}{12}$

Note

You may rationalize the denominator by multiplying by $\frac{\sqrt{8}}{\sqrt{8}}$ . It is more efficient to simplify the radical first.

$\frac{7 \sqrt[3]{3}}{\sqrt[3]{9 y}}$

$\frac{7 \sqrt[3]{3}}{\sqrt[3]{3^{2} y}} (\frac{\sqrt[3]{3 y^{2}}}{\sqrt[3]{3 y^{2}}}) \frac{7 \sqrt[3]{9 y^{2}}}{\sqrt[3]{3^{3} y^{3}}}$

$\frac{7 \sqrt[3]{9 y^{2}}}{3 y}$

$\frac{5 + x}{x + \sqrt{5}}$

$\frac{5 + x}{x + \sqrt{5}} (\frac{x - \sqrt{5}}{x - \sqrt{5}}) \frac{5 x - 5 \sqrt{5} + x^{2} - x \sqrt{5}}{x^{2} - 5}$

$\frac{x^{2} + 5 x - x \sqrt{5} - 5 \sqrt{5}}{x^{2} - 5}$

Note

Q: What is the conjugate of the denominator?

A: $x - \sqrt{5}$

If you wrote the terms in a different order, it is still correct. However, it is standard to write terms in descending order by degree.

$\frac{7 x}{2 - 2 \sqrt{x}}$

$\frac{7 x}{2 - 2 \sqrt{x}} (\frac{2 + 2 \sqrt{x}}{2 + 2 \sqrt{x}}) \frac{14 x + 14 x \sqrt{x}}{4 - 4 x} \frac{2 (7 x + 7 x \sqrt{x})}{2 (2 - 2 x)} \frac{2 (7 x + 7 x \sqrt{x})}{2 (2 - 2 x)}$

$\frac{7 x + 7 x \sqrt{x}}{2 - 2 x}$

Note

Q: If all coefficients are even, what should be simplified (factored) out of all terms?

A: A factor of at minimum 2.

$\frac{\sqrt[4]{3 y^{2}}}{\sqrt[4]{8 x^{2}}}$

$\frac{\sqrt[4]{3 y^{2}}}{\sqrt[4]{2^{3} x^{2}}} (\frac{\sqrt[4]{2 x^{2}}}{\sqrt[4]{2 x^{2}}}) \frac{\sqrt[4]{6 x^{2} y^{2}}}{\sqrt[4]{2^{4} x^{4}}}$

$\frac{\sqrt[4]{6 x^{2} y^{2}}}{|2 x|}$

Note

You need to multiply the problem by the radical that will make the denominator simplify to a non-radical expression. Since the index is 4, the radicand needs to be an expression that will result in $\sqrt[4]{2^{4} x^{4}}$ when multiplied by the given denominator.

$\frac{4}{- 3 - \sqrt{7}}$

$\frac{4}{- 3 - \sqrt{7}} (\frac{- 3 + \sqrt{7}}{- 3 + \sqrt{7}}) \frac{- 12 + 4 \sqrt{7}}{9 - 7} \frac{- 12 + 4 \sqrt{7}}{2}$

$- 6 + 2 \sqrt{7}$

Note

Q: Why does the sign of –3 not change when working with conjugates?

A: Because only the symbol between the terms changes.

$\frac{11 + \sqrt{3}}{\sqrt{2} - \sqrt{3}}$

$\frac{11 + \sqrt{3}}{\sqrt{2} - \sqrt{3}} (\frac{\sqrt{2} + \sqrt{3}}{\sqrt{2} + \sqrt{3}}) \frac{11 \sqrt{2} + 11 \sqrt{3} + \sqrt{6} + 3}{2 - 3} \frac{11 \sqrt{2} + 11 \sqrt{3} + \sqrt{6} + 3}{- 1}$

$- 11 \sqrt{2} - 11 \sqrt{3} - \sqrt{6} - 3$

Note

Distribute the denominator –1 across all terms to simplify completely.

$- \sqrt{6} (3 \sqrt{2} - 4 \sqrt{3})$

$- 3 \sqrt{12} + 4 \sqrt{18} - 3 \sqrt{2^{2} \cdot 3} + 4 \sqrt{2 \cdot 3^{2}} - 3 (2) \sqrt{3} + 4 (3) \sqrt{2}$

$- 6 \sqrt{3} + 12 \sqrt{2}$

The area of a rectangle is $7 + \sqrt{2}$ square inches, and the length is $6 - \sqrt{2}$ inches. Determine the simplified width.

$\begin{array}{rcl} A & = & l w \\ \frac{A}{l} & = & w \\ w & = & \frac{7 + \sqrt{2}}{6 - \sqrt{2}} \\ = & \frac{7 + \sqrt{2}}{6 - \sqrt{2}} (\frac{6 + \sqrt{2}}{6 + \sqrt{2}}) \\ = & \frac{42 + 13 \sqrt{2} + 2}{36 - 2} \end{array}$

$\frac{44 + 13 \sqrt{2}}{34}$

Note

Remember to rationalize the denominator.

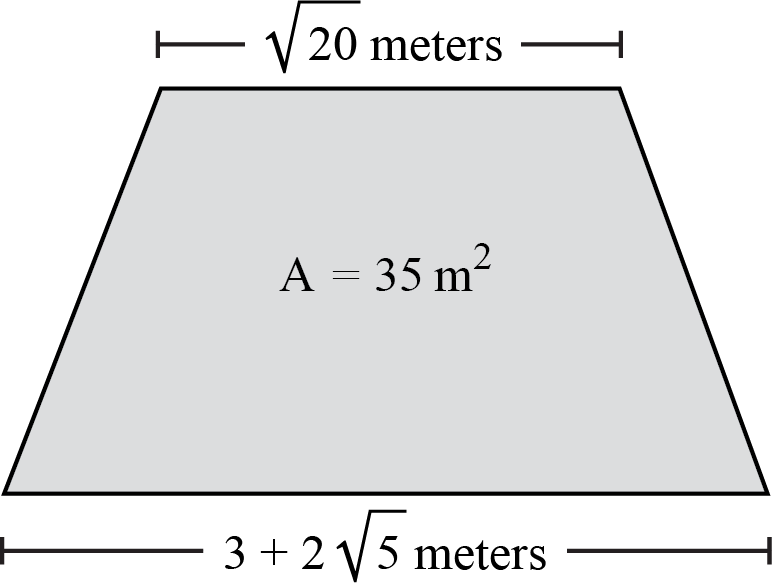
The bases of a trapezoid are $3 + 2 \sqrt{5}$ meters and $\sqrt{20}$ meters. If the area of the trapezoid is 35 square meters, determine the height of the trapezoid.

$\begin{array}{rcl} A & = & \frac{1}{2} h (b_{1} + b_{2}) \\ h & = & \frac{2 A}{b_{1} + b_{2}} \\ h & = & \frac{2 (35)}{(3 + 2 \sqrt{5}) + (\sqrt{20})} \\ = & \frac{70}{3 + 2 \sqrt{5} + 2 \sqrt{5}} \\ = & \frac{70}{3 + 4 \sqrt{5}} \\ = & \frac{70}{3 + 4 \sqrt{5}} (\frac{3 - 4 \sqrt{5}}{3 - 4 \sqrt{5}}) \\ = & \frac{210 - 280 \sqrt{5}}{3 - 16 (5)} \\ = & \frac{210 - 280 \sqrt{5}}{3 - 80} \\ = & \frac{210 - 280 \sqrt{5}}{- 77} \\ = & \frac{7 (30 - 40 \sqrt{5})}{7 (- 11)} \\ = & \frac{7 (30 - 40 \sqrt{5})}{7 (- 11)} \end{array}$

$h = \frac{- 30 + 40 \sqrt{5}}{11} meters$

Use the given figure to answer problems 11–12.

The Neills are fencing in a rectangular pasture for their goats and need to know the area that will have grass for the goats to eat.

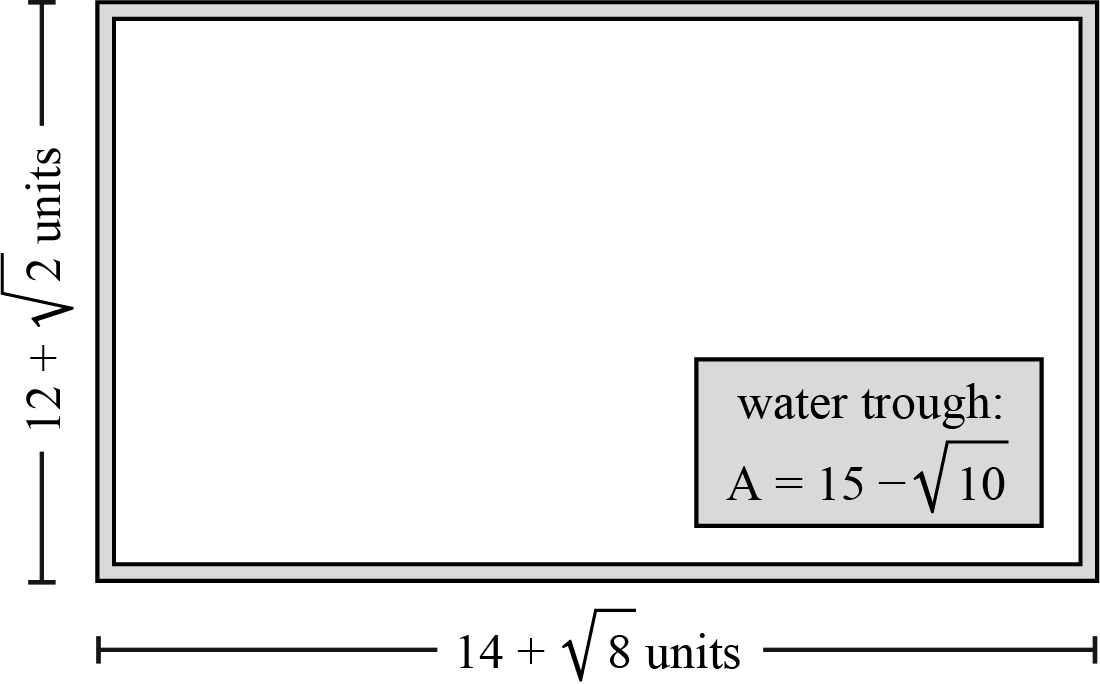
If a water trough with an area of $15 - \sqrt{10}$ square units is added to the enclosure, what is the total area of pasture the goats will be able to use?

$\begin{array}{rcl} A & = & l w \\ A_{yard} & = & (14 + \sqrt{8}) (12 + \sqrt{2}) \\ = & 168 + 14 \sqrt{2} + 12 \sqrt{8} + \sqrt{16} \\ = & 168 + 14 \sqrt{2} + 24 \sqrt{2} + 4 \\ = & 172 + 38 \sqrt{2} \end{array}$
$\begin{array}{rcl} A_{goats} & = & A_{yard} - A_{trough} \\ = & 172 + 38 \sqrt{2} - (15 - \sqrt{10}) \\ = & 172 + 38 \sqrt{2} - 15 + \sqrt{10} \end{array}$

$A_{goats} = 157 + 38 \sqrt{2} + \sqrt{10} {units}^{2}$

Knowing that the goats would soon eat all of the available grass in the fenced in area, the Neills decided to extend both the length and width by $4 + \sqrt{2}$ units. What is the new total area of pasture the goats will be able to use?
(Hint: The water trough is still in the fenced area.)

$\begin{array}{rcl} New Length & = & (14 + \sqrt{8}) + (4 + \sqrt{2}) \\ = & 14 + 2 \sqrt{2} + 4 + \sqrt{2} \\ = & 18 + 3 \sqrt{2} \end{array}$

$\begin{array}{rcl} New Width & = & (12 + \sqrt{2}) + (4 + \sqrt{2}) \\ = & 16 + 2 \sqrt{2} \end{array}$

$\begin{array}{rcl} New area of yard : \\ A & = & l w \\ A & = & (18 + 3 \sqrt{2}) (16 + 2 \sqrt{2}) \\ = & 228 + 36 \sqrt{2} + 48 \sqrt{2} + 6 \sqrt{4} \\ = & 228 + 84 \sqrt{2} + 12 \\ = & 240 + 84 \sqrt{2} \end{array}$

Total area for the goats = Total area – Area of the water trough

$\begin{array}{rcl} A_{goats} & = & 240 + 84 \sqrt{2} - (15 + \sqrt{10}) \\ = & 240 + 84 \sqrt{2} - 15 + \sqrt{10} \end{array}$

$A_{goats} = 225 + 84 \sqrt{2} - 15 + \sqrt{10} {units}^{2}$