Practice 2 Solutions

Simplify. Rationalize the denominator. Assume all variables are positive.

$\frac{13}{\sqrt[3]{12}}$

$\frac{13}{\sqrt[3]{2^{2} \cdot 3}} (\frac{\sqrt[3]{2 \cdot 3^{2}}}{\sqrt[3]{2 \cdot 3^{2}}}) \frac{13 \sqrt[3]{18}}{2 \cdot 3}$

$\frac{13 \sqrt[3]{18}}{6}$

$\frac{3 x - \sqrt{2}}{3 x + \sqrt{2}}$

$\frac{3 x - \sqrt{2}}{3 x + \sqrt{2}} (\frac{3 x - \sqrt{2}}{3 x - \sqrt{2}}) \frac{9 x^{2} - 3 x \sqrt{2} - 3 x \sqrt{2} + \sqrt{4}}{9 x^{2} - 2}$

$\frac{9 x^{2} - 6 x \sqrt{2} + 2}{9 x^{2} - 2}$

$\frac{11 \sqrt{2}}{\sqrt{3}}$

$\frac{11 \sqrt{2}}{\sqrt{3}} (\frac{\sqrt{3}}{\sqrt{3}})$

$\frac{11 \sqrt{6}}{3}$

$\frac{10 + 2 \sqrt{7}}{5 + \sqrt{7}}$

$\frac{2 (5 + \sqrt{7})}{5 + \sqrt{7}} \frac{2 (5 + \sqrt{7})}{5 + \sqrt{7}}$

Note

$5 + \sqrt{7}$ simplifies from the expression. Rationalizing the denominator will yield the same solution; however, it is efficient to simplify the expression prior to rationalizing.

$\frac{3 \sqrt[3]{3}}{\sqrt[3]{{(2 x)}^{2}}}$

$\frac{3 \sqrt[3]{3}}{\sqrt[3]{{(2 x)}^{2}}} (\frac{\sqrt[3]{2 x}}{\sqrt[3]{2 x}}) \frac{3 \sqrt[3]{6 x}}{\sqrt[3]{{(2 x)}^{3}}}$

$\frac{3 \sqrt[3]{6 x}}{2 x}$

$\frac{9 x^{2} \sqrt{3 y}}{\sqrt{20 x^{3} y}}$

$\frac{9 x^{2} \sqrt{3 y}}{2 x \sqrt{5 y}} = \frac{9 x^{2} \sqrt{3 y}}{2 x \sqrt{5 y}} = \frac{9 x \sqrt{3}}{2 \sqrt{5}} \frac{9 x \sqrt{3}}{2 \sqrt{5}} (\frac{\sqrt{5}}{\sqrt{5}}) \frac{9 x \sqrt{15}}{2 \cdot 5}$

$\frac{9 x \sqrt{15}}{10}$

Note

It is most efficient to simplify the radical prior to rationalizing. The x’s simplify since they are both outside the radicand, and the y’s simplify because they are both inside the radicand.

$\frac{- 2 + x}{- 7 - \sqrt{17}}$

$\frac{- 2 + x}{- 7 - \sqrt{17}} (\frac{- 7 + \sqrt{17}}{- 7 + \sqrt{17}}) \frac{14 - 2 \sqrt{17} - 7 x + x \sqrt{17}}{49 - 17}$

$\frac{14 - 2 \sqrt{17} - 7 x + x \sqrt{17}}{32}$

$9 \sqrt[3]{4} (\sqrt[3]{6} + \sqrt[3]{2}) + 18$

$9 \sqrt[3]{24} + 9 \sqrt[3]{8} + 18 9 \sqrt[3]{2^{3} \cdot 3} + 9 \sqrt[3]{2^{3}} + 18 9 \cdot 2 \sqrt[3]{3} + 9 \cdot 2 + 18 18 \sqrt[3]{3} + 18 + 18$

$18 \sqrt[3]{3} + 36$

Determine the area, in simplified radical form, of the gray region only.

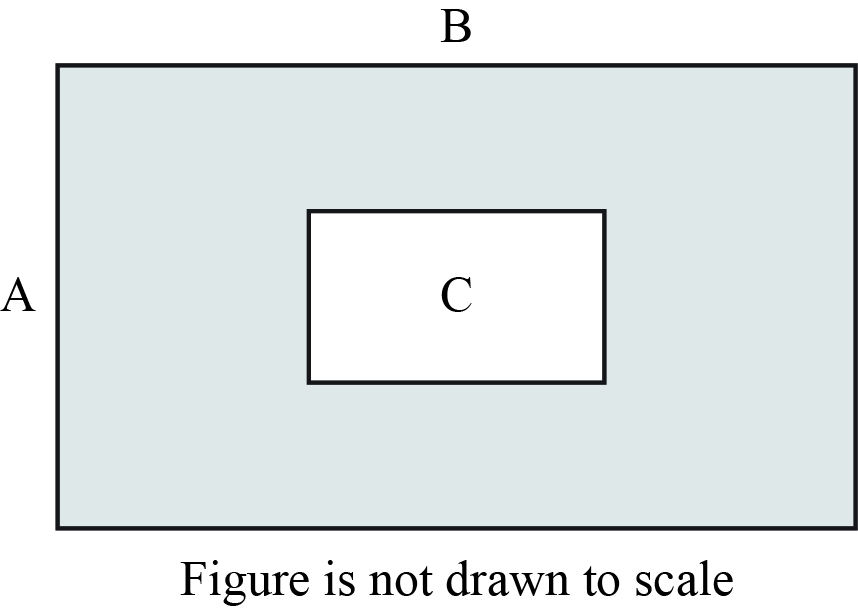
$A = 3 \sqrt{7} + 2 \sqrt{5} units B = 4 \sqrt{7} - \sqrt{5} units C = 2 + 2 \sqrt{35} {units}^{2}$

$A B - C (3 \sqrt{7} + 2 \sqrt{5}) (4 \sqrt{7} - \sqrt{5}) - (2 + 2 \sqrt{35}) 12 (7) - 3 \sqrt{35} + 8 \sqrt{35} - 2 (5) - 2 - 2 \sqrt{35} 84 + 3 \sqrt{35} - 10 - 2$

Note

Q: How can you determine the area of the gray region only?

A: Find the total area of the gray rectangle and subtract the area of rectangle C from it.

$72 + 3 \sqrt{35} {units}^{2}$

The area of a triangle is 14 square meters and the height of the triangle is $2 \sqrt{3}$ meters. Find the base in simplified radical form.

$\begin{array}{rcl} A & = & \frac{1}{2} b h \\ b & = & \frac{2 A}{h} \\ = & \frac{2 (14)}{2 \sqrt{3}} \\ = & \frac{2 (14)}{2 \sqrt{3}} \\ = & \frac{14}{\sqrt{3}} (\frac{\sqrt{3}}{\sqrt{3}}) \end{array}$

$b = \frac{14 \sqrt{3}}{3} meters$

The formula for the area of a hexagon is $A = \frac{1}{2} a n s$ where n is the number of sides of the figure. Find the area of a hexagon if the apothem is $5 \sqrt{3}$ feet and the length of one side is 5.

$A = \frac{1}{2} a n s A = \frac{1}{2} (5 \sqrt{3}) (6) (5)$

$A = 75 \sqrt{3} {ft}^{2}$

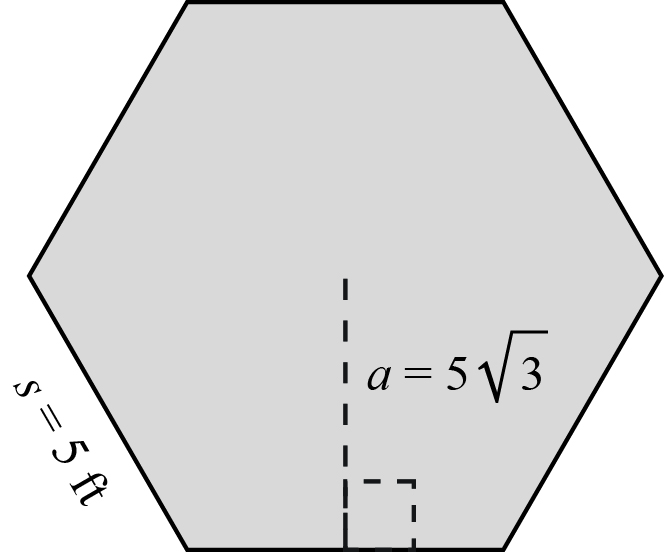
Note

The apothem is the perpendicular distance from the side of the figure to its center.

The area of a rectangle is $75 + \sqrt{5} {ft}^{2}$ and the length is $25 - \sqrt{5}$ feet. Determine the width in simplified radical form.

$\begin{array}{rcl} A & = & l w \\ w & = & \frac{A}{l} \\ w & = & \frac{75 + \sqrt{5}}{25 - \sqrt{5}} \\ = & \frac{75 + \sqrt{5}}{25 - \sqrt{5}} (\frac{25 + \sqrt{5}}{25 + \sqrt{5}}) \\ = & \frac{1875 + 100 \sqrt{5} + 5}{625 - 5} \\ = & \frac{1880 + 100 \sqrt{5}}{620} \\ = & \frac{20 (94 + 5 \sqrt{5})}{20 (31)} \\ = & \frac{20 (94 + 5 \sqrt{5})}{20 (31)} \end{array}$

$w = \frac{94 + 5 \sqrt{5}}{31} ft$