Explore: Transforming Reciprocal Functions Solutions

Transforming Reciprocal Functions Solutions

Recall from Algebra 1, the following is true of transformations of parabolas: 
- a reflects, stretches, and compresses a graph.
- h shifts a graph left or right.
- k shifts a graph up or down.

Changes to a, h , and k are transformations on the reciprocal parent function across the coordinate plane.

Reflections, Stretches, and Compressions

The value of a will determine the location of the graph relative to the asymptotes . 
The value of a also determines if the graph is a reflection , and if it is stretched or compressed. 
- A reflection flips the graph into the region opposite of the parent graph.  
- Stretching will move the graph away from the asymptotes. 
- Compression will move the graph toward the asymptotes.

If a is negative ( –a) the graph is reflected .
$g (x) = - \frac{1}{x}, x \neq 0$

a = –1, h = 0, k = 0

If $|a| > 0$ , the graph will stretch vertically.
$h (x) = \frac{5}{x}, x \neq 0$

a = 5, h = 0, k = 0

If $0 < |a| < 1$ , the graph will compress vertically.
$j (x) = \frac{1}{5 x}, x \neq 0$
$a = \frac{1}{5}, h = 0, k = 0$

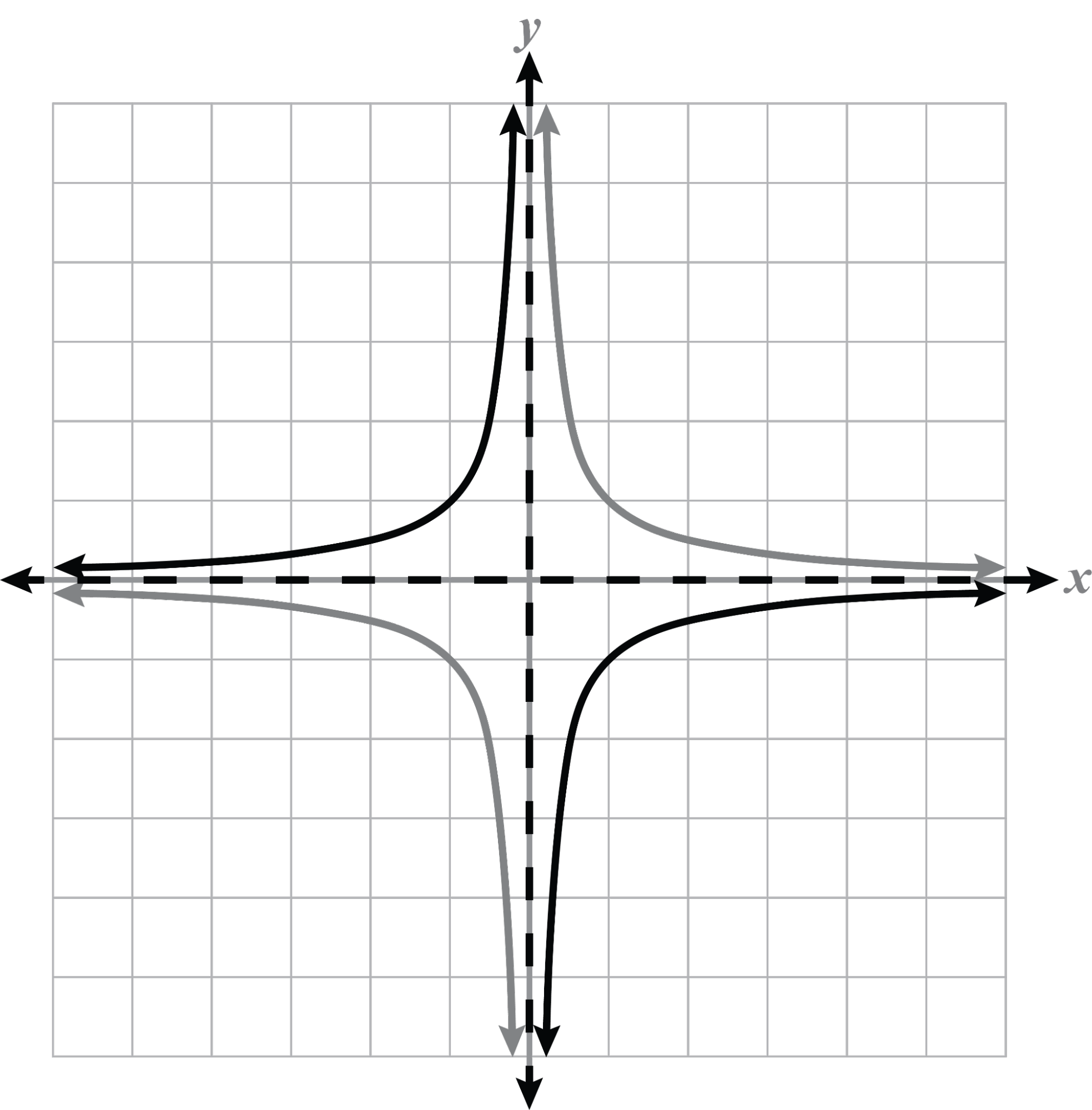
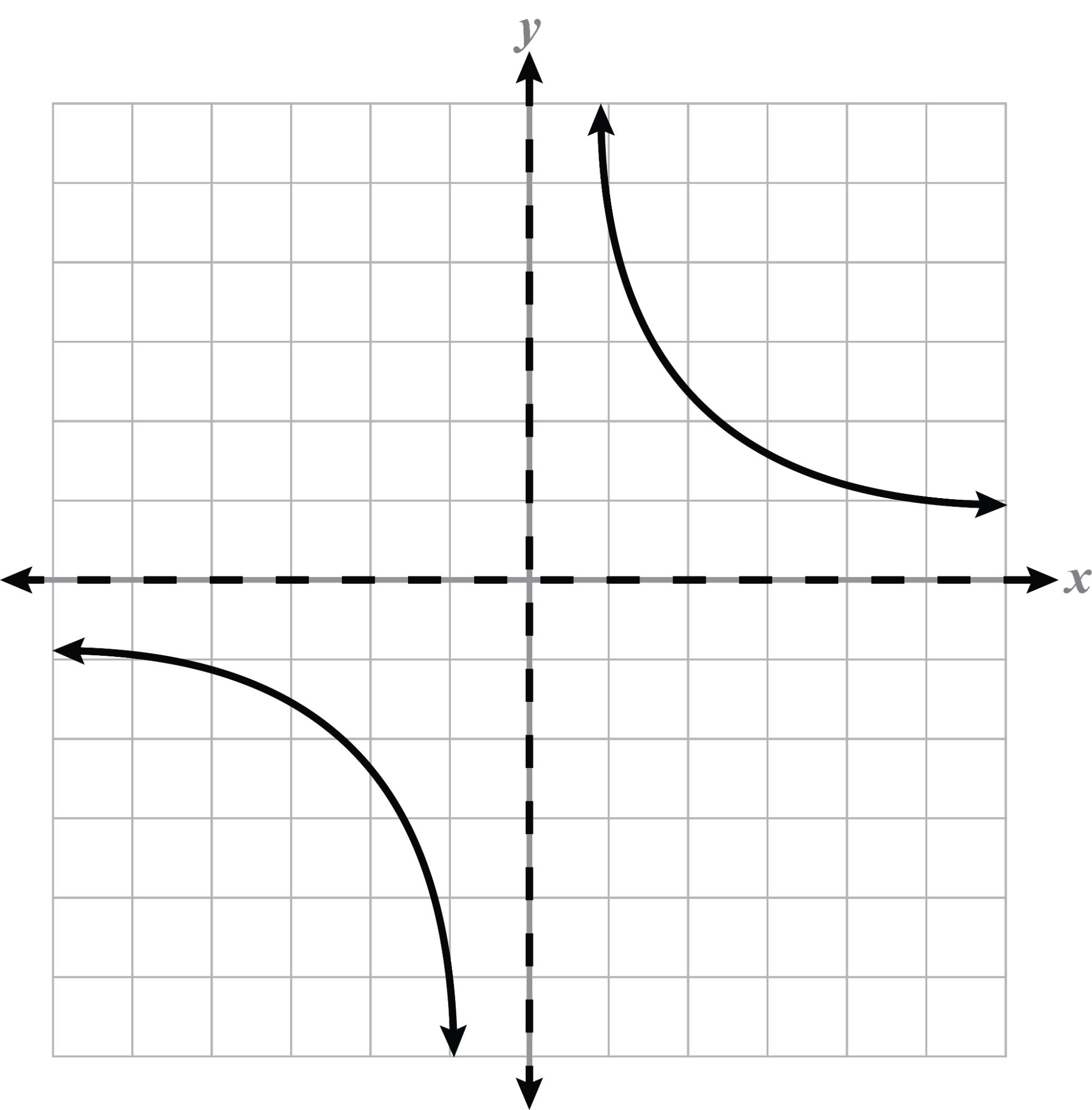
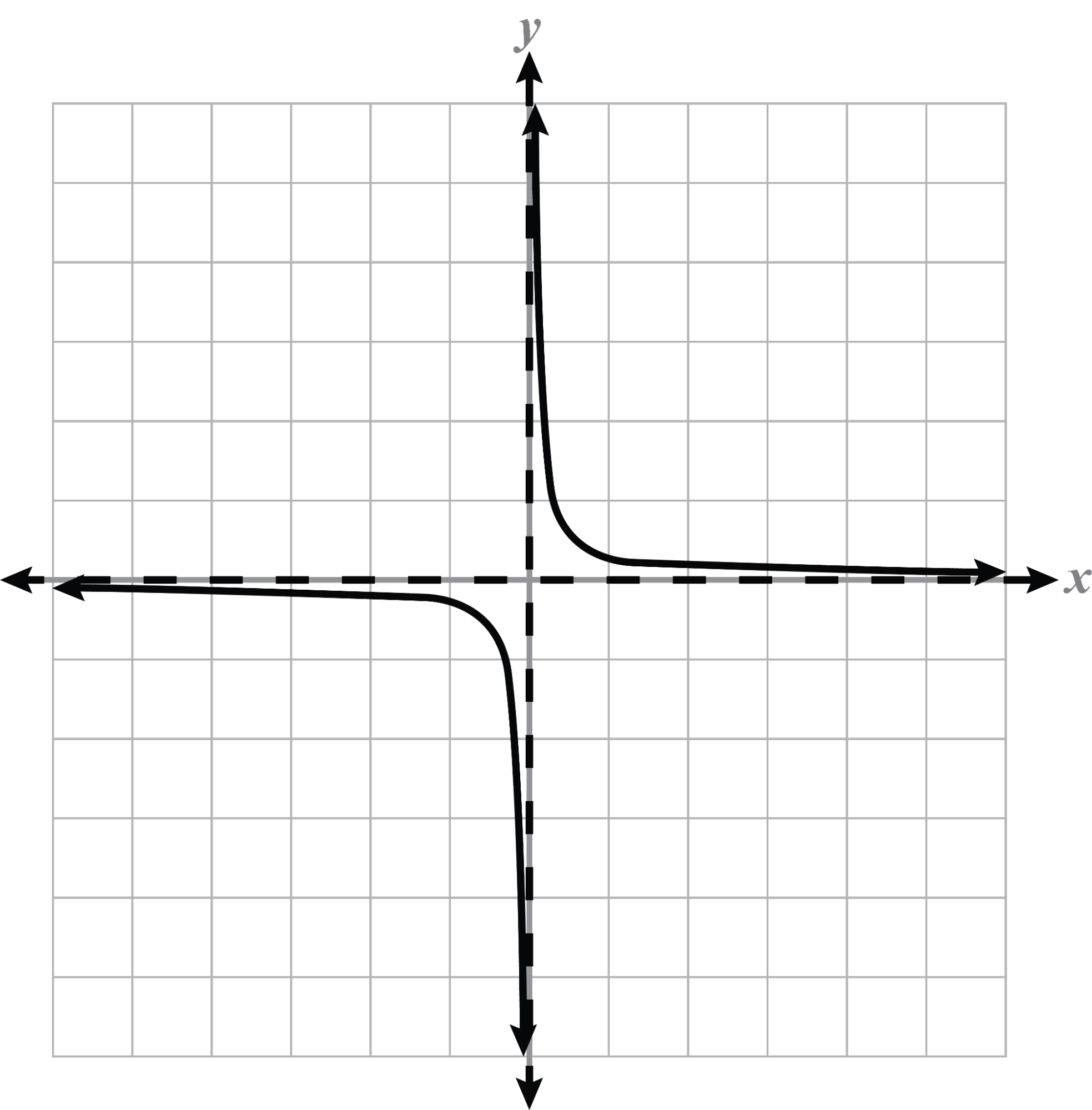
Note

Use the More to Explore activity to go deeper with technology.

Horizontal and Vertical Shifts

(x – h) moves the graph right →
(The h-value is positive) 
(x + h) moves the graph left ←
(The h-value is negative) 
+k moves the graph up ↑  
–k moves the graph down ↓

$g (x) = \frac{1}{x + 2} - 1, x \neq - 2 a = 1, h = - 2, k = - 1$

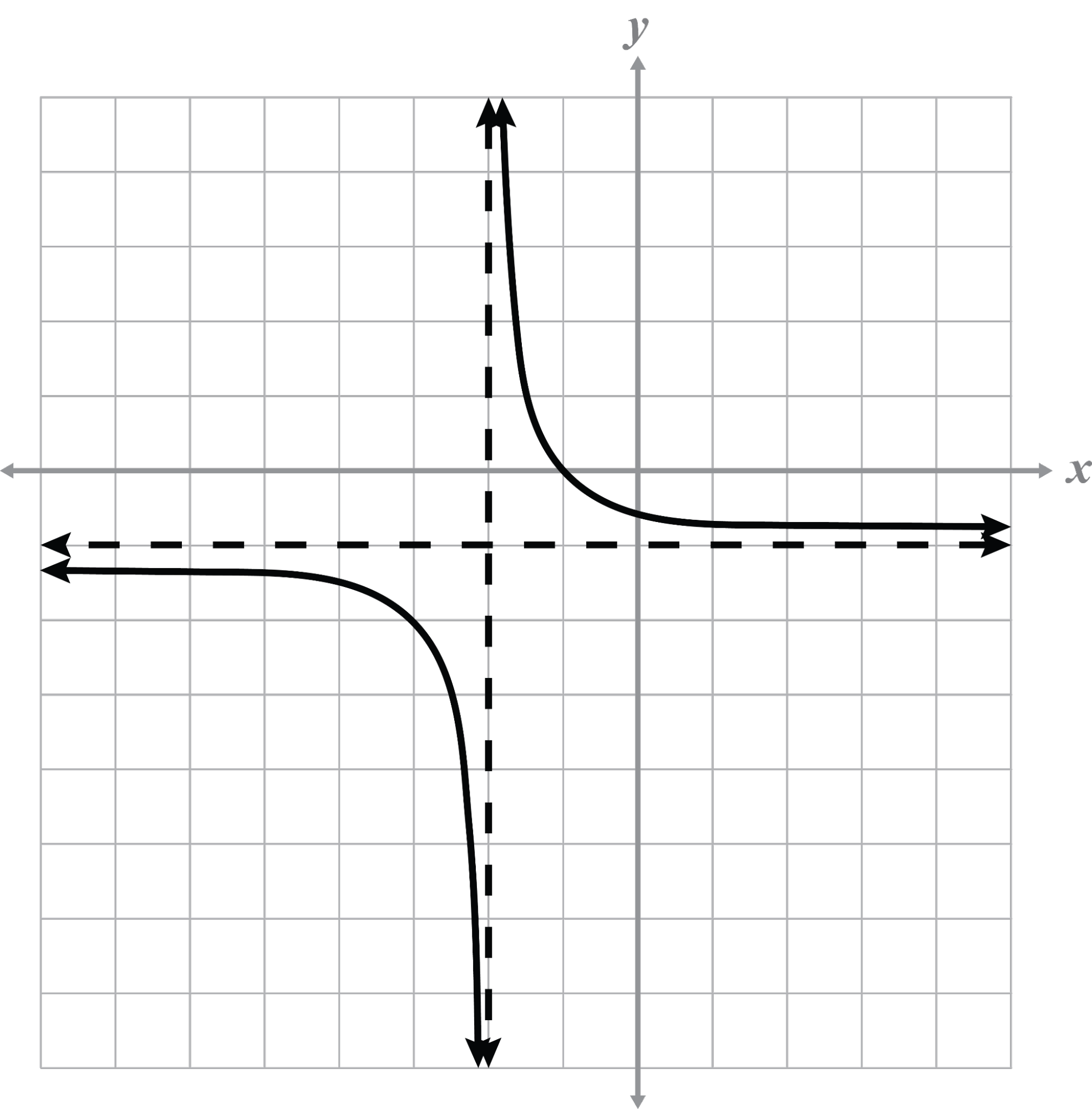
Example 1

Name any asymptotes and intercepts from the given graph. Describe the transformation from the parent graph.

$g (x) = \frac{1}{x - 2} + 1, x \neq 2$

Plan
Name a, h, k 

Name the equations for the asymptotes 

Calculate the intercepts algebraically 

Describe the transformation of the graph 

Implement

$a = 1, h = 2, k = 1$

Note

The directions do not explicitly state to identify a, h, k; however, it is good practice for working with any reciprocal function, as it helps determine the characteristics of the graph.

Asymptotes: (read from the graph)
$x = 2 y = 1$
Intercepts: (estimate from graph, confirm algebraically)

x-intercept:

$\begin{array}{rcl} 0 & = & \frac{1}{x - 2} + 1 \\ - 1 & = & \frac{1}{x - 2} \\ - 1 (x - 2) & = & 1 \\ - x + 2 & = & 1 \\ - x & = & - 1 \\ x & = & 1 \\ (1, 0) \end{array}$

y-intercept:

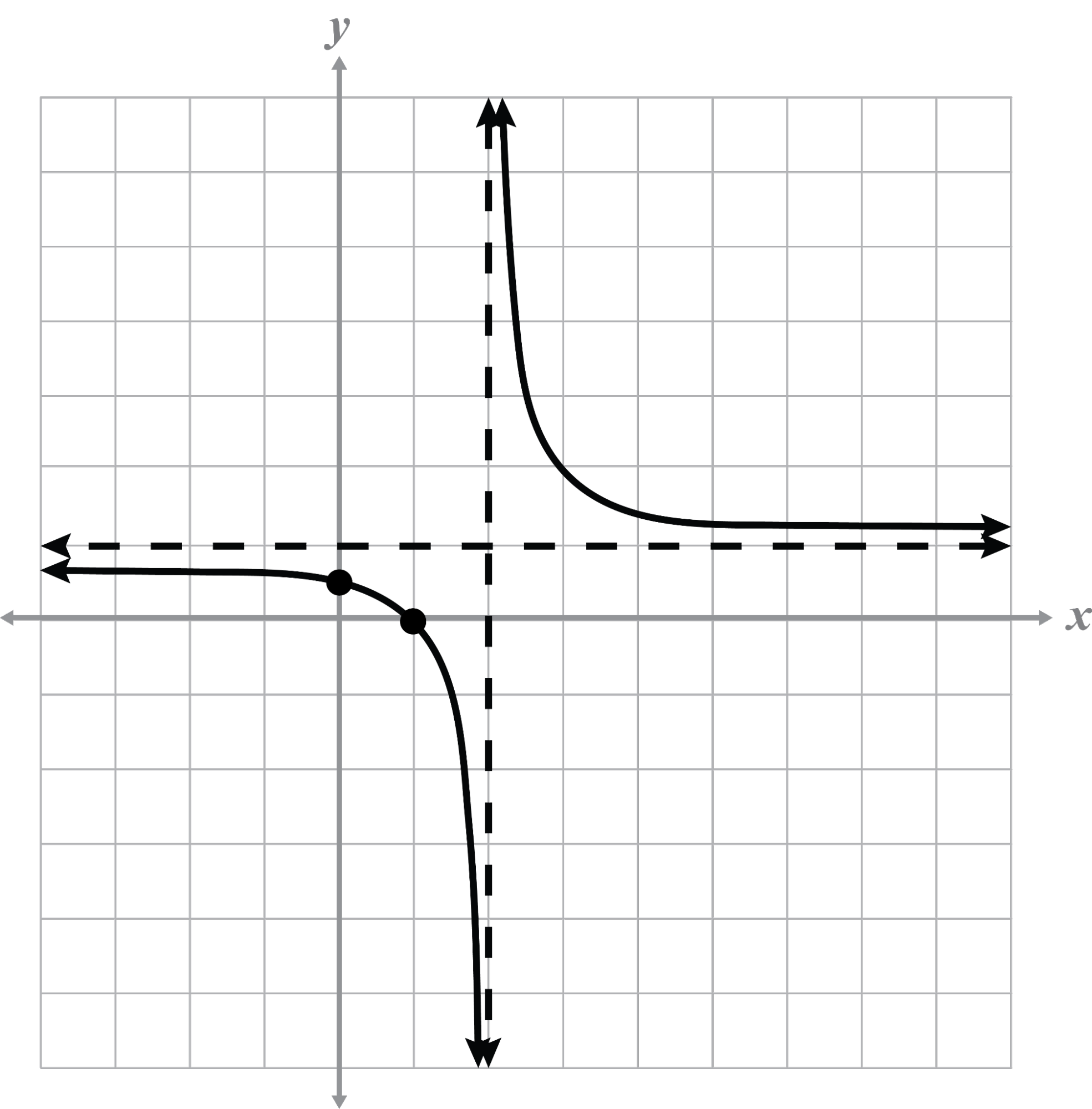
$\begin{array}{rcl} f (0) & = & \frac{1}{0 - 2} + 1 \\ = & - \frac{1}{2} + 1 \\ = & \frac{1}{2} \\ (0, \frac{1}{2}) \end{array}$

Some graphs will not have intercepts because the graph does not cross either axis.

Note

Determine intercepts algebraically because the result is often a fraction or decimal value. It is too difficult to correctly identify the intercepts from only reading the graph.

Explain

g(x) is two spaces right and one space up from the parent graph because h = 2, k = 1, and a = 1.

Example 2

Name any asymptotes and intercepts from the given graph. Describe the transformation from the parent graph.

$q (x) = - \frac{3}{x} + 2, x \neq 0$

$a = - 3, h = 0, k = 2$

Asymptotes: (read from graph)

x = 0

y = 2

Intercepts: (estimate from graph, confirm algebraically)

x-intercept:

$\begin{array}{rcl} 0 & = & - \frac{3}{x} + 2 \\ - 2 & = & \frac{- 3}{x} \\ - 2 x & = & - 3 \\ x & = & \frac{3}{2} \\ (1.5, 0) \end{array}$

y-intercept:

none

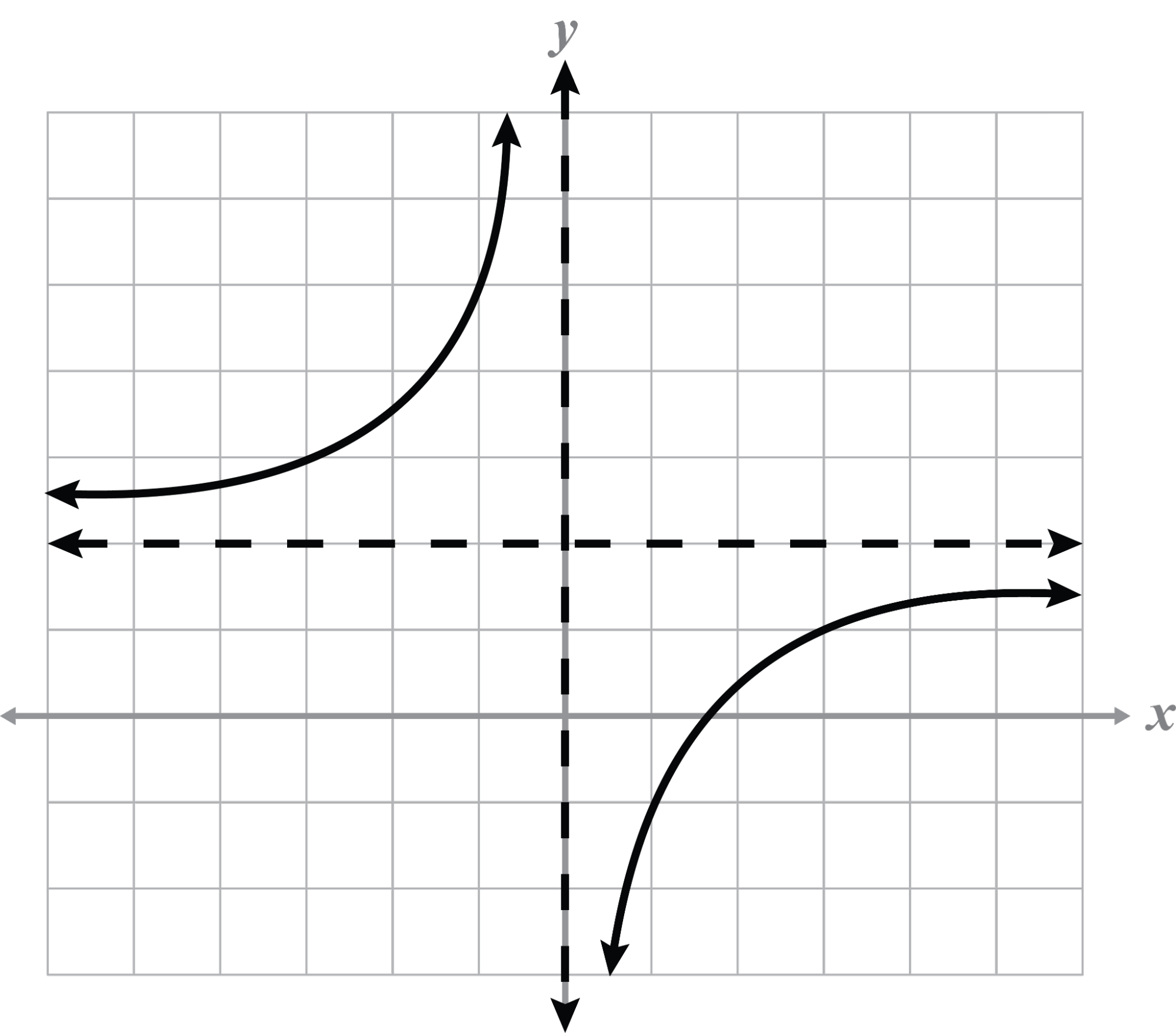
This graph is reflected and stretched vertically because $a = - 3 .$ The graph is shifted up two spaces because $k = 2 .$

Example 3

Name any asymptotes and intercepts from the given graph. Describe the transformation from the parent graph.

$h (x) = \frac{1}{x + 3}, x \neq - 3$

$a = 1, h = - 3, k = 0$

Asymptotes:

Note

You can either do the work or read from the graph.

x = –3
y = 0

Intercepts:

Note

You can estimate from a graph and/or confirm algebraically.

x-intercept:

none

y-intercept:

$h (0) = \frac{1}{0 + 3} = \frac{1}{3} (0, \frac{1}{3})$

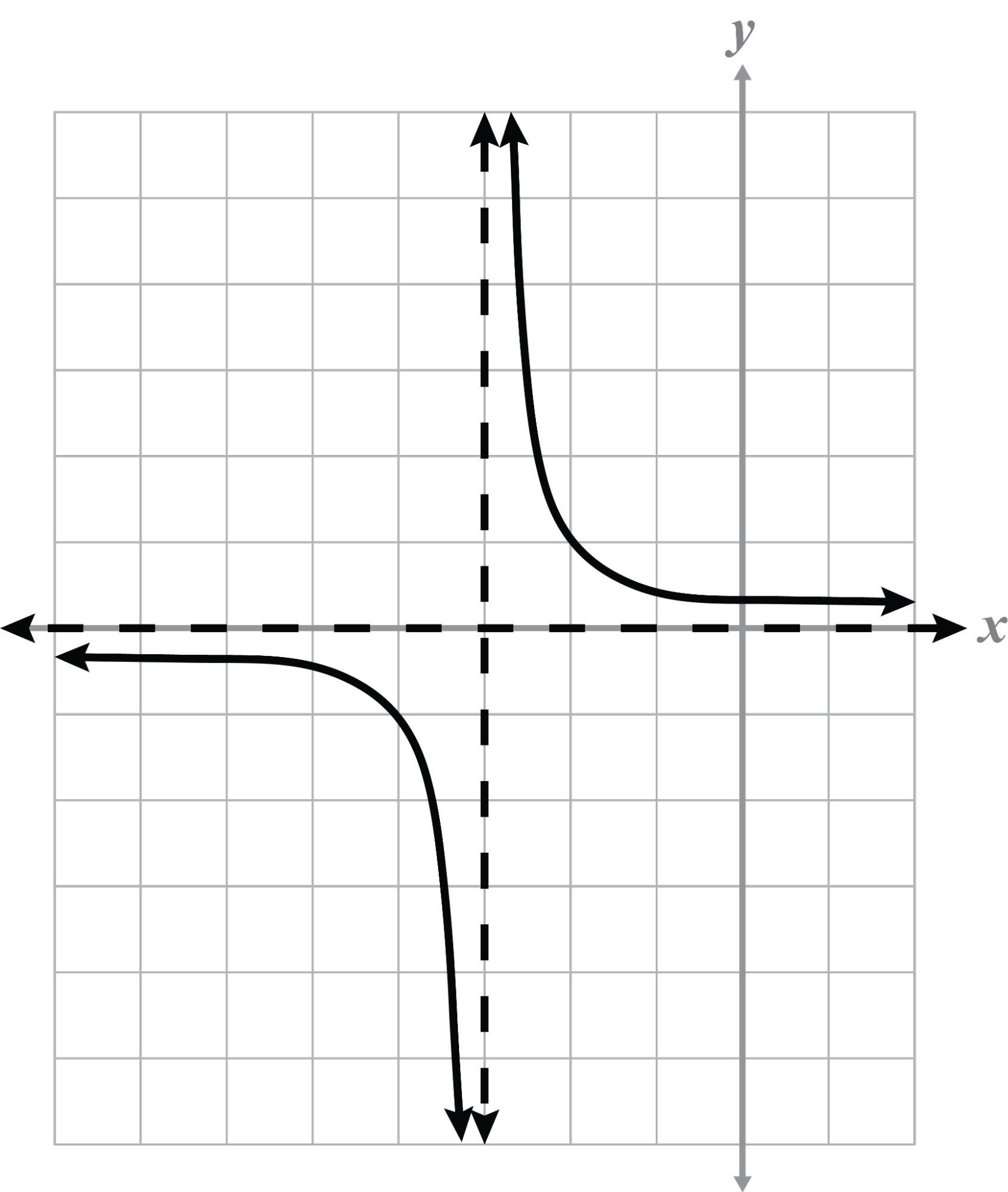
The graph h(x) shifts 3 spaces left compared to the parent function because $h = - 3, k = 0,$ and $a = 1 .$