Unit 1 Test (Lessons 1–10) Solutions

#	Answer	Lesson Origin
1A)	$\frac{1}{50} + \frac{1}{75} = \frac{1}{t}$ Sara and Liz will be able to complete the shopping in 30 minutes.	9, 7
1B)	Sara will maximize truck space with the vertex (18, 10).	1
1C)	The area of the base is $\frac{x + 5}{3 x - 2}$ square inches.	7, 8
2)	C	3, 9
3)	A	3, 5
4)	D	8
5)	B	5
6)	A	2
7)	B	2
8)	C	3, 4
9)	A	3, 8
10)	D	3, 5
11)	D	3, 4
12)	B	10
13)	A	1
14)	B	7
15)	A	3, 10
16)	A	3
17)	C	3, 9
18)	D	5, 6
19)	A	3, 8, 9
20)	B	5, 6
21)	B	10
22)		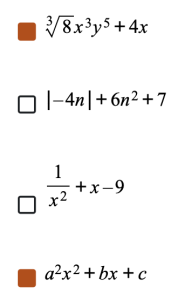3
23)		1
24)		3, 7, 8
25)		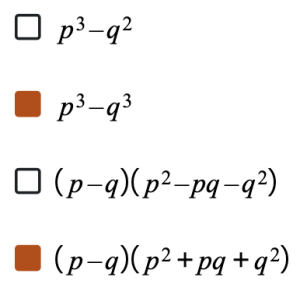3

Sara and Liz are going grocery shopping for a family party.
1. It takes Sara 50 minutes to shop and Liz 75 minutes using the same list. How quickly will Sara and Liz be able to complete their grocery trip if they work together? Write and solve a rational equation.

	Sara		Liz		Together
time	50		75		t
rate	$\frac{1}{50}$	+	$\frac{1}{75}$	=	$\frac{1}{t}$

$\begin{array}{rcl} \frac{1}{50} + \frac{1}{75} & = & \frac{1}{t} LCD (50, 75, t) = 150 t \\ \frac{1}{50} (\frac{3 t}{3 t}) + \frac{1}{75} (\frac{2 t}{2 t}) & = & \frac{1}{t} (\frac{150}{150}) \\ 3 t + 2 t & = & 150 \\ 5 t & = & 150 \\ t & = & 30 \end{array}$

Sara and Liz will be able to complete the shopping in 30 minutes.

Sara wanted to maximize trunk space in the car to fit all of the groceries. Using a system of linear inequalities, the vertices {(0, 10), (12, 20), (18, 10), (9, 0)} were determined by mapping the trunk on the coordinate plane.

Determine the maximum trunk space using the objective function $f (x, y) = x + \frac{1}{2} y$ .

$f (0, 10) = (0) + \frac{1}{2} (10) f (0, 10) = 5 minimum$

$f (12, 20) = (12) + \frac{1}{2} (20) f (12, 20) = 22$

$f (18, 10) = (18) + \frac{1}{2} (10) f (18, 10) = 23 maximum$

$f (9, 0) = (9) + \frac{1}{2} (0) f (9, 0) = 9$

Sara will maximize trunk space with the vertex (18, 10).

The volume of one grocery bag is $\frac{2 x^{2} + 7 x - 15}{3 x^{2} - 13 x - 10}$ cubic inches.

If the height of the grocery bag is $\frac{2 x - 3}{x - 5}$ inches, what is the area of the base when V = lwh?

$V = l w h \frac{V}{h} = l w$

$\frac{\frac{2 x^{2} + 7 x - 15}{3 x^{2} - 13 x - 10}}{\frac{2 x - 3}{x - 5}} = \frac{2 x^{2} + 7 x - 15}{3 x^{2} - 13 x - 10} \div \frac{2 x - 3}{x - 5} x \neq - \frac{2}{3}, 5, \frac{3}{2} l w = \frac{(2 x - 3) (x + 5)}{(3 x + 2) (x - 5)} \cdot \frac{x - 5}{2 x - 3} l w = \frac{x + 5}{3 x - 2} square inches$

The area of the base is $\frac{x + 5}{3 x - 2}$ square inches.

Which equation is equivalent to the given equation?
$\frac{x + 3}{3 x} = \frac{x + 4}{x - 4}$

$x + 1 = - 1$
$2 x - 1 = 4 x + 4$
$x^{2} - x - 12 = 3 x^{2} + 12 x$
$x^{2} + 7 x + 12 = 3 x^{2} - 12 x$

Cross Product:

$\begin{array}{rcl} (x + 3) (x - 4) & = & 3 x (x + 4) \\ x^{2} - x - 12 & = & 3 x^{2} - 12 x \end{array}$

Note

This option “crosses out” terms without adhering to math rules.
This option is the cross sum rather than cross product (not equivalent).
This option is the product of the numerator and denominator (not equivalent).

Simplify:
$(8 x^{3} y^{2} - 5 x^{2} y^{2} + 12 x y + 7) {(2 x y)}^{- 1}$

$4 x^{2} y - \frac{5 x y}{2} + 6 + \frac{7}{2 x y}$
$6 x^{2} y - 3 x y + 10 + \frac{5}{x y}$
$\frac{4}{x^{2} y} - \frac{5}{2 x y} + 6 - \frac{7}{2 x y}$
$16 x^{4} y^{3} - 10 x^{3} y^{3} + 20 x^{2} y^{2} + 14 x y$

$\frac{8 x^{3} y^{2}}{2 x y} - \frac{5 x^{2} y^{2}}{2 x y} + \frac{12 x y}{2 x y} + \frac{7}{2 x y}$

Note

Coefficients of fractions cannot be subtracted.
Variable placement must follow exponent rules.
The terms are multiplied rather than divided.

Name the least common denominator for the polynomials:
$\frac{1}{2 m + 2}, \frac{3}{m^{2} + m}, and \frac{1}{m + 1}$

$2 m$
$m + 1$
$m^{2} + 3 m + 3$
$2 m^{2} + 2 m$

$\begin{array}{rcl} 2 m + 2 & = & 2 (m + 1) \\ m^{2} + m & = & m (m + 1) \\ m + 1 & = & m + 1 \\ LCD : 2 m (m + 1) \end{array}$

Note

This option is the product of the GCF of the first two expressions.
This option is the binomial that is part of the LCM.
This option is the sum of the given expressions.

Choose the statement that best completes the sentence about division.
When completing polynomial long division in which the quotient contains no remainder, ___.

the division problem was incorrectly simplified.
the quotient is a factor of the dividend.
the dividend has no factors.
nothing can be determined.

Note

When two expressions are divided and there is no remainder, this means the quotient is a factor. (e.g., $\frac{10}{5} = 2$ , 2 is a factor of 10)

The sum of three numbers is zero. The sum of the first and second numbers is negative six. The product of –2 and the first number equals the third number plus four. Determine the system of equations that best represents the problem.

$x + y + z = 0 x + y = - 6 - 2 x = z + 4$
$x + y + z = 0 x y = - 6 - 2 (x + z) = 4$
$x + y + z = 0 x + y = - 6 - 2 x = x + 4$
$x + y + z = 0 x - y = - 6 - 2 x = z + 4$

Note

The second equation shows the product of terms. The third equation should not multiply x and z by –2.
The last equation does not use the third variable.
The middle equation is the difference of the first two terms.

Determine the sum of the first and third terms, x and z, for the system:
$x - y + z = - 8 x + y = 12 y - z = 6$

20
6
–10
12

Note

This option is the sum of y and z.
This option is the sum of x and y.
This option is the difference between x and z.

$\begin{array}{rcl} x - y + z = - 8 + y - z = 6 x = - 2 2 (- 2) + z = 4 - 4 + z = 4 z = 8 \end{array}$ $x - y + z = - 8 + x + y = 12 2 x + z = 4 x - y + z = - 8 (- 2) - y + (8) = - 8 6 - y = - 8 y = 14$

$(- 2, 14, 8)$

$x + z (- 2) + (8) 6$

Determine the expression equivalent to
${(x - 4)}^{2}$ to form a polynomial identity.

$(x - 4) (x + 4) + (x - 3) (x + 3)$
${(x - 5)}^{2} - {(x - 1)}^{2}$
${(2 x - 5)}^{2} + (12 x - 9 - 3 x^{2})$
${(2 x - 5)}^{2} - 3 x^{2} + 9$

${(x - 4)}^{2} = x^{2} - 8 x + 16$

Note

This expression simplifies to $2 x^{2} - 25$ . These are a difference of squares, not trinomial squares.
This expression simplifies to –8x = 24. The constants cannot be subtracted until the binomials are squared.
This expression simplifies to $x^{2} - 20 x + 34$ .

Find the perimeter of a triangle with sides $2 x - 5, \frac{x - 8}{x + 4}$ , and $\frac{3}{x} .$

$\frac{2 x^{3} + 4 x^{2} - 25 x + 12}{x (x + 4)}$
$\frac{3 x - 10}{2 x + 4}$
$\frac{3 x - 14}{x}$
$\frac{2 x^{2} - 15 x + 25}{(x + 4) (2 x - 5)}$

$LCD : x (x + 4) 2 x - 5 + \frac{x - 8}{x + 4} + \frac{3}{x} \frac{x (x + 4) (2 x - 5)}{x (x + 4)} + \frac{x (x - 8)}{x (x + 4)} + \frac{3 (x + 4)}{x (x + 4)} (x^{2} + 4 x) (2 x - 5) + x^{2} - 8 x + 3 x + 12 2 x^{3} - 5 x^{2} + 8 x^{2} - 20 x + x^{2} - 8 x + 3 x + 12 2 x^{3} + 4 x^{2} - 25 x + 12$

Note

The terms are combined in the numerator and denominator without using an LCD.
This option subtracts 4 from the numerator and denominator and ignores rules about using an LCD.
This option is the answer when $(2 x - 5) (x + 4)$ is used as the LCD.

Simplify: $(4 x^{3} + 5 x + 1) \div (2 x^{2} - x + 3)$

$2 x + 1$
$2 x + 1 + \frac{10 x - 2}{2 x^{2} - x + 3}$
$2 x + 1 - \frac{2}{2 x^{2} - x - 3}$
$2 x + 1 - \frac{1}{x^{2} - x + 3}$

$2 x^{2} - x + 3 2 x + 1 4 x^{3} + 0 x^{2} + 5 x + 1 - (4 x^{3} - 2 x^{2} + 6 x) 2 x^{2} - x + 1 - (2 x^{2} - x + 3) - 2 + \frac{(- 2)}{2 x^{2} - x + 3}$

Note

The remainder is missing from the answer.
6x is not subtracted in the first step.
2 cannot be simplified from the remainder and its divisor.

Determine the value(s) of Q that will make a polynomial identity for ${(2 x + Q)}^{2} = Q (4 x + 8) + 4 x^{2} - Q .$

–7, 0
0
7
0, 7

$\begin{array}{rcl} 4 x^{2} + 4 Q x + Q^{2} & = & 4 Q x + 8 Q + 4 x^{2} - Q \\ 4 x^{2} + 4 Q x + Q^{2} & = & 4 x^{2} + 4 Q x + 7 Q \\ Q^{2} & = & 7 Q \\ Q^{2} - 7 Q & = & 0 \\ Q (Q - 7) & = & 0 \\ Q & = & 0, 7 \end{array}$

Note

This option has the opposite sign for one value of Q.

B–C) These options represent only one of the two values for Q.

Describe the transformation of the rational function $h (x) = \frac{1}{x + 6} - 8$ , as compared to the parent function $f (x) = \frac{1}{x} .$

The graph shifts right 6 spaces and down 8 spaces.
The graph shifts left 6 spaces and down 8 spaces.
The graph shifts right 6 spaces and up 8 spaces.
The graph shifts left 6 spaces and up 8 spaces.

Note

A, C) $(x + h)$ shifts the graph left.

C, D) –k shifts the graph down.

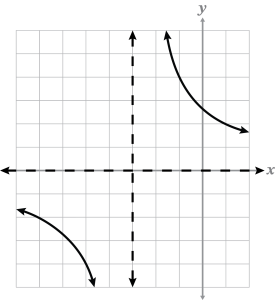
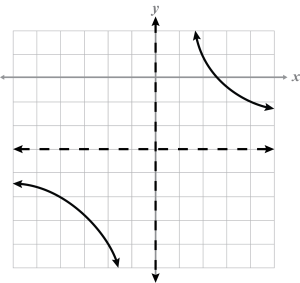
Which region best represents the system of linear inequalities: $x \geq 0, y \geq 0, x + y \geq 5, 2 x + y \leq 8$

Region A
Region B
Region C
Region D

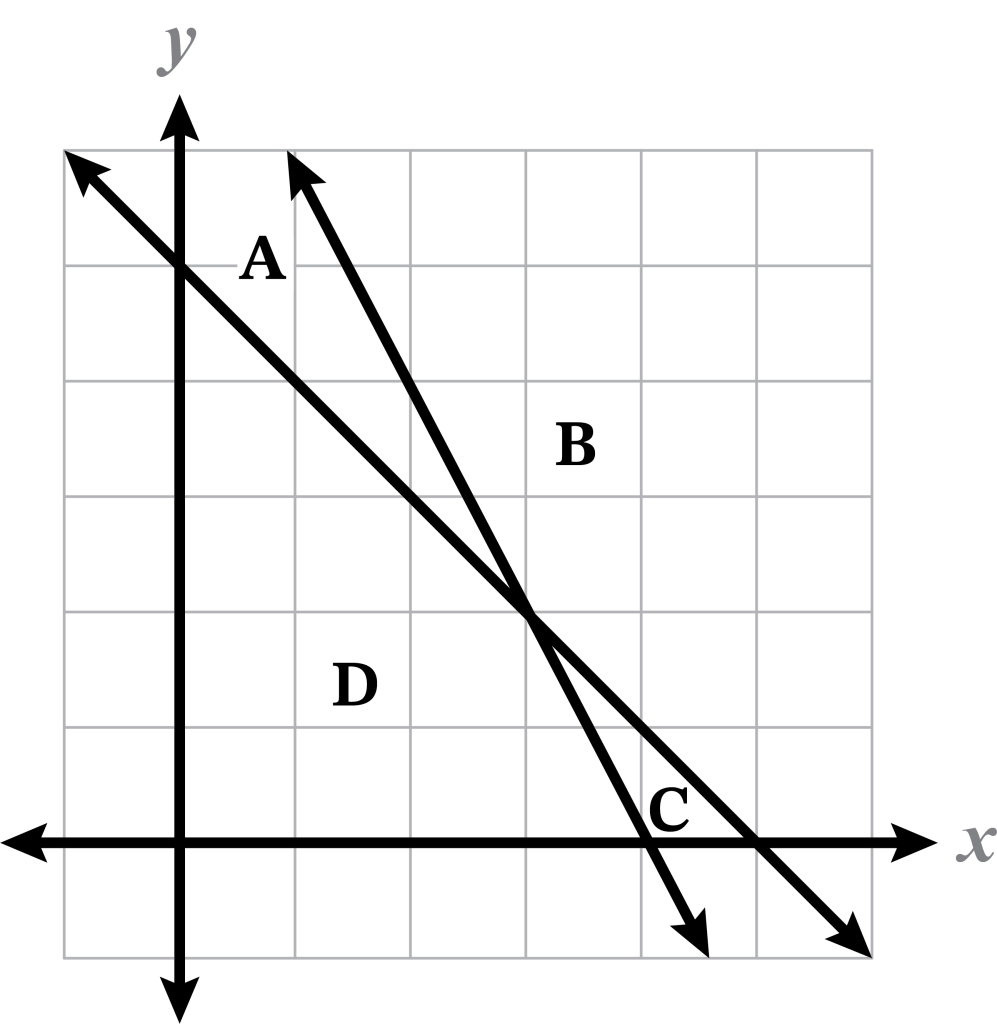
Note

B, C, D) Only region A is true for all inequalities of the system.

$Region A : (1, 6) 1 + 6 \geq 5 ✓ 2 (1) + 6 \leq 8 ✓$

$Region B : (5, 5) 5 + 5 \geq 5 ✓ 2 (5) + 5 \leq 8 ✖$

$Region C : (5.5, 0.5) 5.5 + 0.5 \geq 5 ✓ 2 (5.5) + 0.5 \leq 8 ✖$

$Region D : (1, 1) 1 + 1 \geq 5 ✖ 2 (1) + 1 \leq 8 ✓$

Simplify: $\frac{x^{2} + 3 x - 10}{x^{2} - 6 x + 9} \div \frac{5 x^{2} + 21 x - 20}{x^{2} - 5 x + 6}$

$\frac{2 (x - 2)}{(x - 3) (5 x - 4)}$
$\frac{{(x - 2)}^{2}}{(x - 3) (5 x - 4)}$
$\frac{(5 x - 4) {(x + 5)}^{2}}{{(x - 3)}^{3}}$
$\frac{(x + 5) {(x - 2)}^{2}}{(x - 3) (x - 5) (5 x + 4)}$

$\frac{(x + 5) (x - 2)}{(x - 3) (x - 3)} \div \frac{(5 x - 4) (x + 5)}{(x - 3) (x - 2)} x \neq 3, 2, - 5, \frac{4}{5} \frac{(x + 5) (x - 2)}{(x - 3) (x - 3)} \cdot \frac{(x - 3) (x - 2)}{(5 x - 4) (x + 5)} \frac{{(x - 2)}^{2}}{(x - 3) (5 x - 4)}$

Note

This answer multiplies the numerator by two rather than squaring it.
This is the answer when the reciprocal of the second fraction is not taken.
This is the answer when the signs of the denominator are switched.

State the domain and range for the rational function: $y = \frac{- 3}{x + 12} + 15$

$domain : \{x | x \in ℝ, x \neq - 12\}, range : \{y | y \in ℝ, y \neq 15\}$
$domain : \{x | x \in ℝ, x \neq 12\}, range : \{y | y \in ℝ, y \neq 15\}$
$domain : \{x | x \in ℝ, x \neq 12\}, range : \{y | y \in ℝ, y \neq - 15\}$
$domain : \{x | x \in ℝ, x \neq - 4\}, range : \{y | y \in ℝ, y \neq - 15\}$

$a = - 3, h = - 12, k = 15 x \neq - 12, y \neq 15$

Note

C, D) The value of y has the opposite sign.
B, D) The value of x does not make the denominator zero.

Factor completely: $80 n^{3} + 270$

$10 (2 n + 3) (4 n^{2} - 6 n + 9)$
$10 (2 n + 3) (4 n^{2} + 6 n + 9)$
$10 (2 n + 3) (4 n^{2} - 6 n - 9)$
cannot be factored

$10 (8 n^{3} + 27)$

sum of cubes

$10 (2 n + 3) (4 n^{2} - 6 n + 9)$

Note

The trinomial must have a negative middle term for the sum of cubes.
The trinomial must have a positive last term for the sum of cubes.
The expression can be factored.

Solve: $\frac{5 x + 8}{x + 2} - x = \frac{x}{x + 2}$

$x = - 2$
$x = - 2, 4$
$x = 4$
$x = 2, 4$

$\begin{array}{rcl} \frac{5 x + 8}{x + 2} - \frac{x (x + 2)}{x + 2} & = & \frac{x}{x + 2} LCD : (x + 2), x \neq - 2 \\ 5 x + 8 - x^{2} - 2 x & = & x \\ - x^{2} + 3 x + 8 & = & x \\ 0 & = & x^{2} - 2 x - 8 \\ (x + 2) (x - 4) & = & 0 \\ x & = & - 2, 4 \\ x & = & 4 \end{array}$

Note

A, B) $x = - 2$ is extraneous.

This is the solution if the expression is factored incorrectly.

Divide: $12 y^{3} + 5 y^{2} - 18 y + 4$ by $4 y - 1$

$12 y^{2} + 8 y - 16$
$12 y^{2} + 17 y - 1 + \frac{3}{4 y - 1}$
$3 y^{2} + \frac{1}{2} y - \frac{37}{8} - \frac{\frac{21}{16}}{4 y - 1}$
$3 y^{2} + 2 y - 4$

$\frac{12 y^{3} + 5 y^{2} - 18 y + 4}{4}$ and $\frac{4 y - 1}{4}$

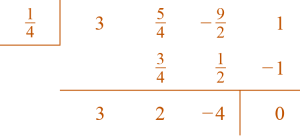
Note

The first step, dividing all terms by the coefficient of the divisor, is skipped.
1 is used in synthetic division rather than $\frac{1}{4}$ .
$- \frac{1}{4}$ is used in synthetic division rather than $\frac{1}{4}$ .

Three people from Miller’s Painting are hired to paint the interior of a house. Each person works at a different rate. The combined rate of the crew is needed to determine how long the job will take. Find the combined working rate of the 3-person crew. $\frac{1}{r}, \frac{1}{r - 2}, \frac{2}{r + 2}$

$\frac{4 r^{2} - 2 r - 4}{r (r - 2) (r + 2)}$
$\frac{4}{3 r}$
$\frac{r^{2} + 2 r - 4}{r (r - 2) (r + 2)}$
$\frac{2 r^{2} - r - 2}{r (r - 1) (r + 1)}$

$\frac{1}{r} + \frac{1}{r - 2} + \frac{2}{r + 2}, LCD : r (r - 2) (r + 2) \frac{1 (r - 2) (r + 2)}{r (r - 2) (r + 2)} + \frac{1 r (r + 2)}{r (r - 2) (r + 2)} + \frac{2 r (r - 2)}{r (r - 2) (r + 2)} r^{2} - 4 + r^{2} + 2 r + 2 r^{2} - 4 r 4 r^{2} - 2 r - 4$

Note

All terms in the numerator and denominator are combined incorrectly because no LCD was used. The numerators cannot be combined unless there is a common denominator.
r is not included in the numerators when finding the LCD.
An attempt is made to simplify out 2 from all terms in the numerator and denominator. This action is incorrect because the GCF of the denominator is 1.

What is the remainder when $x^{3} - 2 x^{2} + 6 x - 8$ is divided by $x - 2$ ?

2
4
–4
–36

$x - 2 = 0, x = 2$

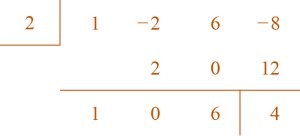
Note

This option occurs if 2 is added, rather than multiplied, by the terms.
This option is the value if the signs of the dividend are switched to their opposites.
This option is the remainder if –2 is used for synthetic division.

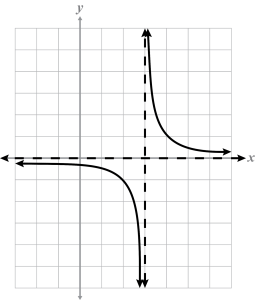
Select the graph that best matches the rational function: $y = \frac{8}{x - 3}$

$a = 8, stretch h = 3, right 3 k = 0$

Note

This graph is not stretched far enough from the asymptotes.
This graph shifts left rather than right.
This graph shifts down 3 rather than right 3.

Select all expressions that represent a polynomial.

$\sqrt[3]{8} x^{3} y^{5} + 4 x$
$|- 4 n| + 6 n^{2} + 7$
$\frac{1}{x^{2}} + x - 9$
$a^{2} x^{2} + b x + c$

Note

Polynomial expressions cannot have a variable in absolute value bars.
Polynomial expressions cannot have variables in the denominator.

Select all that apply.
Optimization is finding the __ value of a function depending on the given parameters of the problem.

ordered pair
minimum
maximum
inequality

Note

The unchecked options do not correctly define optimization.

Select the restrictions for: $\frac{\frac{3 x + 2}{3 x - 1}}{\frac{4 - x}{x}}$

–4
0
4
$\frac{1}{3}$

Note

The value –4 does not make the denominator equal to zero.

$\frac{3 x + 2}{3 x - 1} \div \frac{4 - x}{x} restrictions \begin{matrix} 3 x - 1 = 0 & 4 - x = 0 & x = 0 \\ 3 x = 1 & x = 4 \\ x = \frac{1}{3} \end{matrix} x \neq 0, \frac{1}{3}, 4$

Select all expressions that represent the difference of cubes.

$p^{3} - q^{2}$
$p^{3} - q^{3}$
$(p - q) (p^{2} - p q - q^{2})$
$(p - q) (p^{2} + p q + q^{2})$

Note

The polynomial needs to have both terms to the third power.

The signs are incorrect for the difference of cubes in the trinomial.