Practice 2 Solutions
Given the graph, find the minimum and maximum values using the objective functions.
This problem has one minimum at (2, 3), and one maximum at (7, 3).

This problem has one minimum at (7, 3) and one maximum at (0, 5).

This problem has one minimum at (0, 8) and one maximum at (4, 0).

This problem has one minimum at (0, 2) and one maximum at (6, 2).
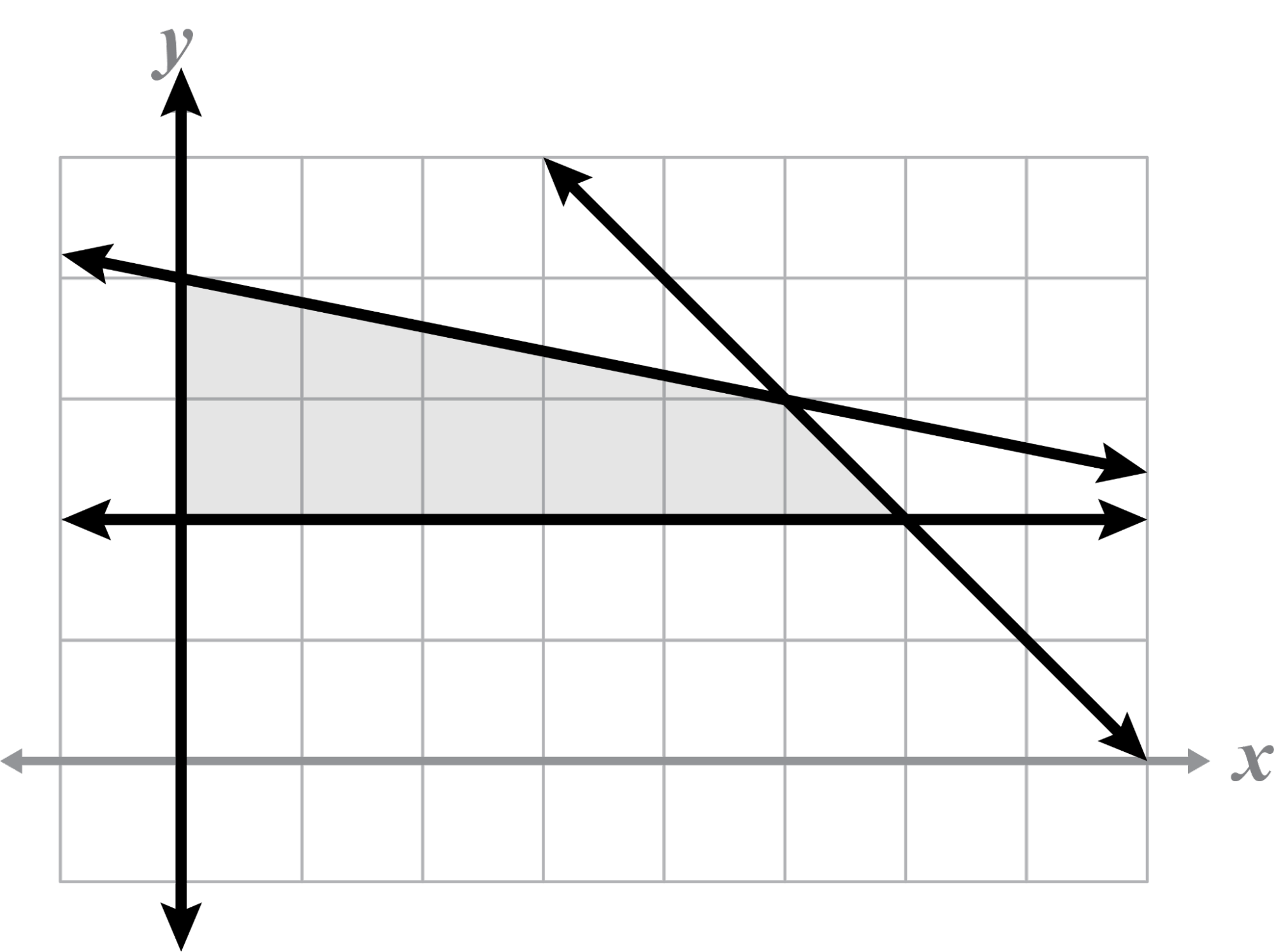
Graph the system of inequalities. Name all of the vertices and evaluate using the objective function for the minimum and maximum values.
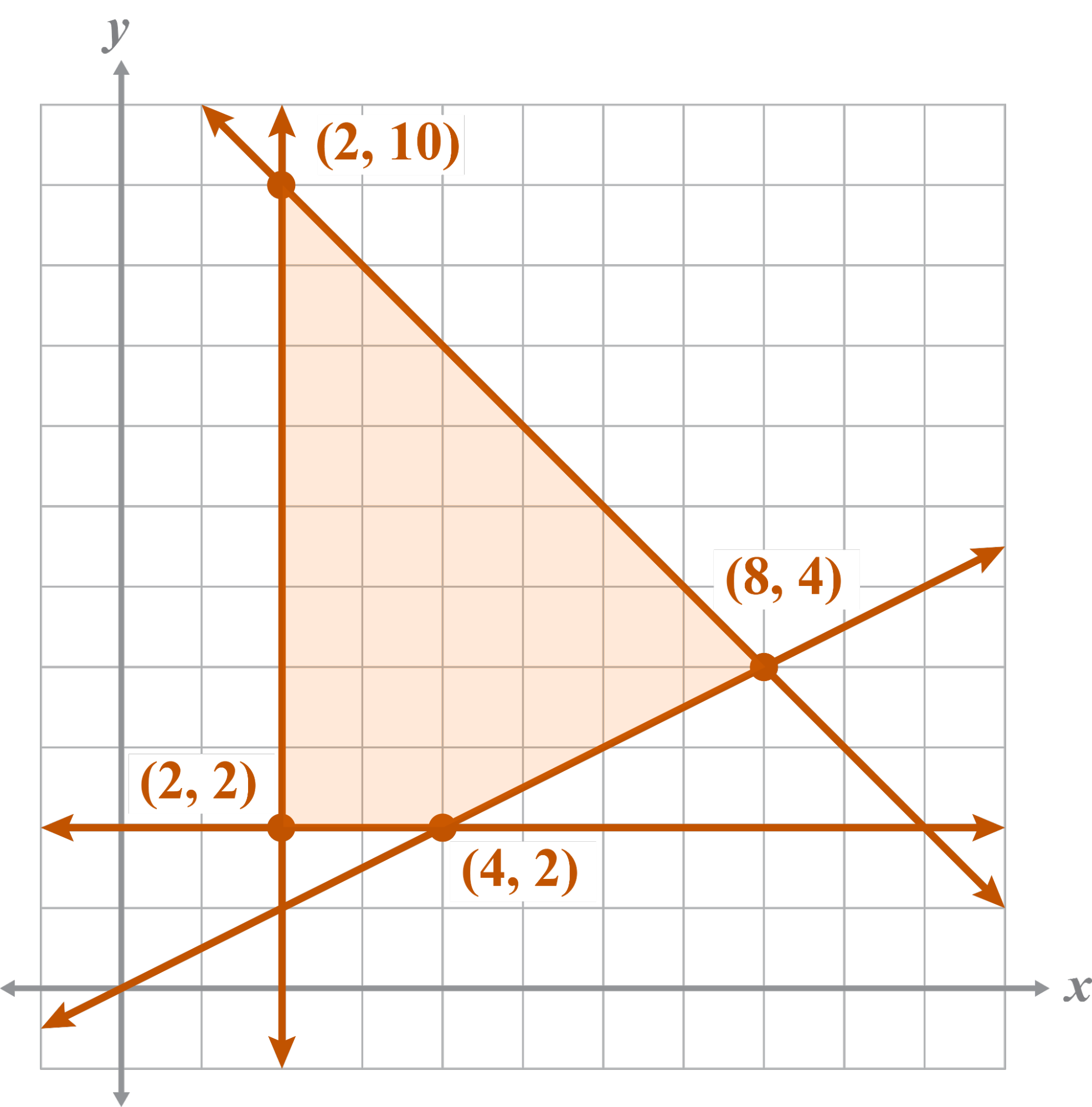
This problem has one minimum at (2, 10) and one maximum at (8, 4).
This problem has one minimum at (0, 6) and one maximum at (15, 0).

This problem has one minimum at (3, 0). This system is unbounded, so there is no maximum.

This problem has one minimum at (0, 1) and one maximum at (8, 1).
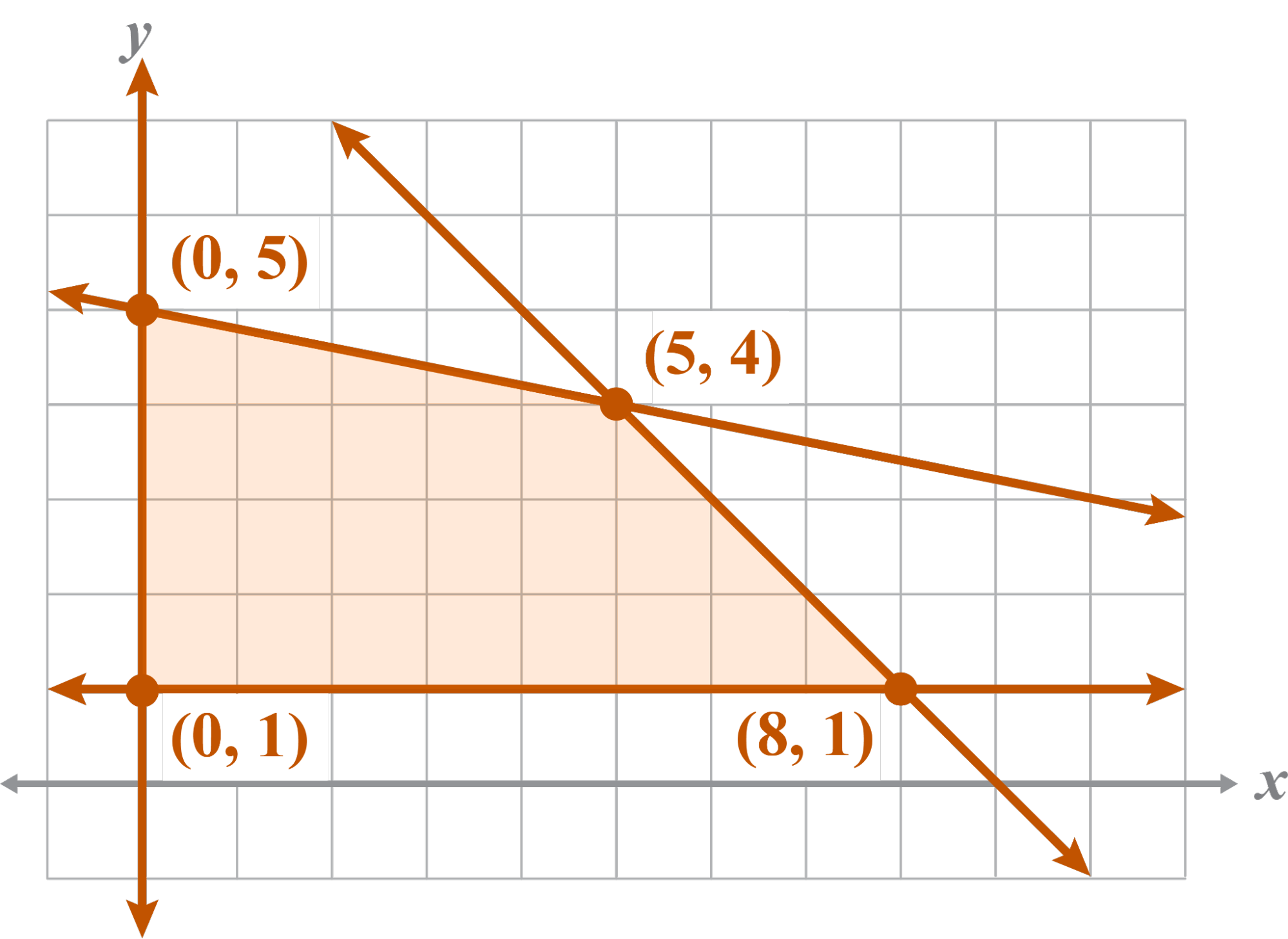
- A food supplier has options for selling almonds and cashews in bulk as a way to save on restaurant food costs. Option A allows restaurants to buy 5-pound bags of almonds and 9-pound bags of cashews with a minimum order of at least $420. Option B allows restaurants to purchase 6-pound bags of almonds and 10-pound bags of cashews with a maximum order of $730. At least 30 pounds of almonds and at least 25 pounds of cashews must be ordered from the food supplier. Determine the minimum purchase when the cost of almonds is $6 per pound and the cost of cashews $8 per pound.
Let x = almonds, y = cashews
Note
Notice that all vertices are on the vertical or horizontal lines. You may substitute y = 25 into and to find the horizontal vertices. Substitute x = 30 into the equations to find the vertical vertices.
To minimize cost, the restaurant should order 30 pounds of almonds and 30 pounds of cashews.

- Sci Labs is producing two new robotic arms. Sci Labs will use at least 20 grams of aluminum and at least 15 grams of iron. Model A uses 30 grams of aluminum and 40 grams of iron and can weigh no more than 2700 grams. Model B uses 20 grams of aluminum and 30 grams of iron and can weigh no more than 1900 grams. Find the maximum number of grams of aluminum and iron Sci Labs should use with the optimization equation
Let x = grams of aluminum
Let y = grams of iron
To have a maximum profit of $3,020 Sci Labs should produce 70 grams of aluminum and 15 grams of iron.

