Targeted Review Solutions
- What is an objective function when working with an optimization problem?
Sample:
The objective function is the function that is used to determine the minimum and maximum for a linear programming problem.
- Determine the least common multiple (LCM) for
Simplify.
Note
Problems 3–4
Recall that a fraction bar represents division. The terms can be stacked vertically (problem 3) or written horizontally (problem 4).
- Factor completely:
- Simplify:
- Bixby’s Bead Shop placed three orders for black, white, and purple beads.
In September, 30 black, 50 white, and 80 purple beads were purchased for $460.
In October, 80 black and 20 white beads were purchased for $260.
In November, $166 was spent on 22 white and 36 purple beads. Write a system with three variables. Do not solve.
- Determine the value of Q that will make the equation a polynomial identity.
Multiple Choice
D
- Determine the range of the function when the domain is all real numbers.
-
all real numbers
-
y ≤ 1
-
y ≥ 0
-
y ≥ 1
The range represents the y-values. The graph approaches the horizontal asymptote, y = 1, and is above this line. This makes the range ≥ 1.
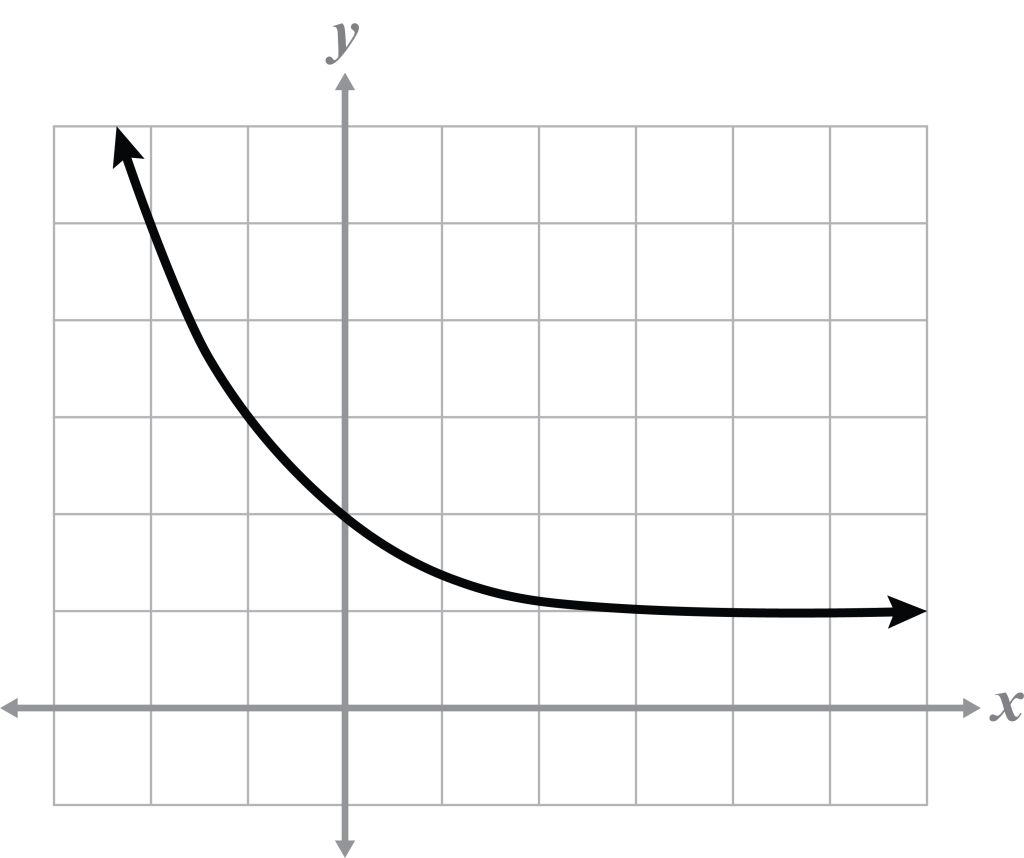
Note
- Exponential functions do not have a range of all real numbers.
- The y-values are above 1, therefore they cannot be less than 1.
- The y-values approach 1, not zero.
D
- Determine the value of (y + z) for the system:
-
16
-
8
-
2
-
–2
Note
Your student should solve for x to find the sum of y and z.
- This option is the value of 2x.
- This option is the value of x.
- This option is the value when the terms are subtracted in the wrong order.
B
- Determine the expression that when set equal to would form a polynomial identity.
-
This is the polynomial identity for the difference of cubes.
Note
- The signs in the second expression are incorrect.
- The coefficients a and b also need to be squared.
- The middle term in the second expression should not have the coefficient 2.
The formula for the difference of cubes is
C
- Select the word that best represents the polynomial.
An expression with three terms with 2 as the highest degree
-
linear binomial
-
linear trinomial
-
quadratic trinomial
-
binomial trinomial
Note
A–B) A linear expression has the highest degree of 1.
- An expression cannot be a binomial and trinomial at the same time.
| Problem | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Origin | L01 | FD | FD | FD | L03 | L03 | L02 | L04 | A1 | L02 | L04 | A1 |
